题目内容
11.在△ABC中,D是边AC的中点,且$AB=1,cosA=\frac{1}{3},BD=\frac{{2\sqrt{3}}}{3}$.(1)求AC的值;
(2)求sinC的值.
分析 (1)由余弦定理列出关系式,将AB,BD的长代入,结合cosA的值解方程即可得到;
(2)由cosA的值,利用同角三角函数间的基本关系求出sinA的值,利用余弦定理表示出cosA,将AB,AC代入求出BC的长,再由AB,BC,sinA的值,利用正弦定理即可求出sinC的值.
解答 解:(1)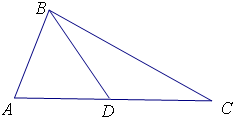 解:(1)在△ABD中,AB=1,BD=$\frac{2\sqrt{3}}{3}$,
解:(1)在△ABD中,AB=1,BD=$\frac{2\sqrt{3}}{3}$,
∴cosA=$\frac{A{B}^{2}+A{D}^{2}-B{D}^{2}}{2AB•AD}$=$\frac{1+A{D}^{2}-\frac{4}{3}}{2AD}$=$\frac{1}{3}$,
解得AD=1,即有AC=2;
(2)cosA=$\frac{1}{3}$,且0<A<π,
∴sinA=$\sqrt{1-co{s}^{2}A}$=$\frac{2\sqrt{2}}{3}$,
又AC=2,
在△ABC中,cosA=$\frac{A{B}^{2}+A{C}^{2}-B{C}^{2}}{2AB•AC}$=$\frac{1+4-B{C}^{2}}{4}$=$\frac{1}{3}$,
解得:BC=$\frac{\sqrt{33}}{3}$,
由正弦定理$\frac{BC}{sinA}$=$\frac{AB}{sinC}$得,sinC=$\frac{ABsinA}{BC}$=$\frac{\frac{2\sqrt{2}}{3}}{\frac{\sqrt{33}}{3}}$=$\frac{2\sqrt{66}}{33}$.
点评 此题考查了正弦、余弦定理,以及同角三角函数间的基本关系,熟练掌握定理是解本题的关键.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
19.设命题p:?x>2,x2>2x,则¬p为( )
| A. | ?x≤2,x2<2x | B. | ?x>2,x2<2x | C. | ?x≤2,x2≤2x | D. | ?x>2,x2≤2x |
16.若$a+\frac{1}{i}=1-bi$(a、b是实数,i是虚数单位),则复数z=a+bi的共轭复数等于( )
| A. | -1-i | B. | -1+i | C. | 1-i | D. | 1+i |