题目内容
证明:“0≤a≤ ”是“函数f(x)=ax2+2(a-1)x+2在区间(-∞,4]上为减函数”的充分不必要条件.
”是“函数f(x)=ax2+2(a-1)x+2在区间(-∞,4]上为减函数”的充分不必要条件.
【答案】分析:利用充分性和必要性的定义证明.
解答:解:当a=0时,f(x)=ax2+2(a-1)x+2=-2x+2,此时函数在定义域上单调递减,所以满足条件.
当a≠0时,要使函数f(x)=ax2+2(a-1)x+2在区间(-∞,4]上为减函数,
则有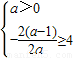 ,即
,即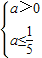 ,所以0≤
,所以0≤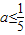 ,
,
综上满足函数f(x)=ax2+2(a-1)x+2在区间(-∞,4]上为减函数的等价条件是0≤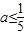 .
.
所以:“0≤a≤ ”是“0≤
”是“0≤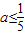 ”成立的充分不必要条件,
”成立的充分不必要条件,
即:“0≤a≤ ”是“函数f(x)=ax2+2(a-1)x+2在区间(-∞,4]上为减函数”的充分不必要条件.
”是“函数f(x)=ax2+2(a-1)x+2在区间(-∞,4]上为减函数”的充分不必要条件.
点评:本题主要考查充分条件和必要条件的判断,先求出命题的等价条件是解决本题的关键.
解答:解:当a=0时,f(x)=ax2+2(a-1)x+2=-2x+2,此时函数在定义域上单调递减,所以满足条件.
当a≠0时,要使函数f(x)=ax2+2(a-1)x+2在区间(-∞,4]上为减函数,
则有
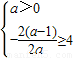 ,即
,即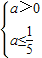 ,所以0≤
,所以0≤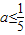 ,
,综上满足函数f(x)=ax2+2(a-1)x+2在区间(-∞,4]上为减函数的等价条件是0≤
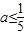 .
.所以:“0≤a≤
 ”是“0≤
”是“0≤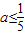 ”成立的充分不必要条件,
”成立的充分不必要条件,即:“0≤a≤
 ”是“函数f(x)=ax2+2(a-1)x+2在区间(-∞,4]上为减函数”的充分不必要条件.
”是“函数f(x)=ax2+2(a-1)x+2在区间(-∞,4]上为减函数”的充分不必要条件.点评:本题主要考查充分条件和必要条件的判断,先求出命题的等价条件是解决本题的关键.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
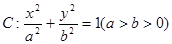 的离心率为
的离心率为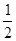 ,以原点为圆心,椭圆的短半轴为半径的圆与直线
,以原点为圆心,椭圆的短半轴为半径的圆与直线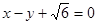 相切.
相切.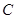 的方程;
的方程;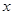 轴对称的任意两个不同的点,连接
轴对称的任意两个不同的点,连接 交椭圆
交椭圆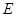 ,证明直线
,证明直线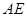 与
与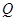 ;
;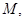
 两点,求
两点,求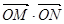 的取值范围.
的取值范围.