题目内容
已知直线 与平面
与平面 平行,P是直线
平行,P是直线 上的一点,平面
上的一点,平面 内的动点B满足:PB与直线
内的动点B满足:PB与直线  成
成 。那么B点轨迹是
。那么B点轨迹是
| A.双曲线 | B.椭圆 | C.抛物线 | D.两直线 |
A
解析试题分析:直线PB与直线  成
成 ,可以过B绕直线l旋转而形成双曲面,被平面
,可以过B绕直线l旋转而形成双曲面,被平面 截后而形成双曲线,故选A。
截后而形成双曲线,故选A。
考点:本题主要考查空间直线与直线所成的角。
点评:简单题,解答本题的关键,是对直线PB的位置进行准确定位。定性地描述,过B绕直线l旋转而形成双曲面。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知抛物线Cl:y2= 2x的焦点为F1,抛物线C2:y=2x2的焦点为F2,则过F1且与F1F2垂直的直线 的一般方程式为
的一般方程式为
| A.2x- y-l=0 | B.2x+ y-1=0 |
| C.4x-y-2 =0 | D.4x-3y-2 =0 |
F1、F2是定点,|F1F2|=6,动点M满足|MF1|+|MF2|=8,则点M的轨迹是( )
| A.线段 | B.直线 | C.椭圆 | D.圆 |
如果函数 的图像与曲线
的图像与曲线 恰好有两个不同的公共点,则实数
恰好有两个不同的公共点,则实数 的取值范围是
的取值范围是
A. | B. | C. | D. |
点 在直线
在直线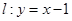 上,若存在过
上,若存在过 的直线交抛物线
的直线交抛物线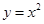 于
于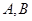 两点,且
两点,且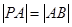 ,则称点
,则称点 为“
为“ 点”,那么下列结论中正确的是( )
点”,那么下列结论中正确的是( )
A.直线 上的所有点都是“ 上的所有点都是“ 点” 点” | B.直线 上仅有有限个点是“ 上仅有有限个点是“ 点” 点” |
C.直线 上的所有点都不是“ 上的所有点都不是“ 点” 点” | D.直线 上有无穷多个点是“ 上有无穷多个点是“ 点” 点” |
抛物线y=x2在点M(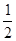 ,
,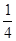 )处的切线的倾斜角是( )
)处的切线的倾斜角是( )
| A.30° | B.45° | C.60° | D.90° |
 的一个焦点与抛物线
的一个焦点与抛物线 的焦点重合,且双曲线的离心率等于
的焦点重合,且双曲线的离心率等于 ,则该双曲线的方程为( )
,则该双曲线的方程为( )



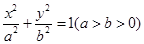 与双曲线
与双曲线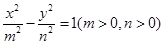 有相同的焦点
有相同的焦点 和
和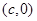 ,若c是a与m的等比中项,n2是2m2与c2的等差中项,则椭圆的离心率为
,若c是a与m的等比中项,n2是2m2与c2的等差中项,则椭圆的离心率为

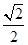
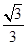
 相切倾斜角为
相切倾斜角为 的直线
的直线 与
与 轴和
轴和 轴的交点分别是A和B,那么过A、B两点的最小圆截抛物线
轴的交点分别是A和B,那么过A、B两点的最小圆截抛物线 C.2 D.
C.2 D.