题目内容
【题目】已知圆![]() ,直线
,直线![]() ,
,![]() .
.
(1)证明:不论![]() 取任何实数,直线
取任何实数,直线![]() 与圆
与圆![]() 恒交于两点;
恒交于两点;
(2)当直线![]() 被圆
被圆![]() 截得的弦长最短时,求此最短弦长及直线
截得的弦长最短时,求此最短弦长及直线![]() 的方程.
的方程.
【答案】(1)见解析(2)最短弦长为![]() .直线
.直线![]() 的方程为
的方程为![]() .
.
【解析】
(1)把直线![]() 的方程变形后,根据直线
的方程变形后,根据直线![]() 恒过定点,得到关于
恒过定点,得到关于![]() 与
与![]() 的二元一次方程组,求出方程组的解即为直线
的二元一次方程组,求出方程组的解即为直线![]() 恒过的定点坐标,然后利用两点间的距离公式求出此点到圆心的距离
恒过的定点坐标,然后利用两点间的距离公式求出此点到圆心的距离![]() ,发现
,发现![]() 小于圆的半径,得到此点在圆内,故直线
小于圆的半径,得到此点在圆内,故直线![]() 与圆恒交于两点;
与圆恒交于两点;
(2)由平面几何知识可知,当直线![]() 与
与![]() 垂直时,所截取的线段最短,由圆心
垂直时,所截取的线段最短,由圆心![]() 和定点
和定点![]() 的坐标求出直线
的坐标求出直线![]() 的斜率,根据两直线垂直时斜率的乘积为
的斜率,根据两直线垂直时斜率的乘积为![]() ,求出直线
,求出直线![]() 的斜率,由
的斜率,由![]() 的坐标和求出的斜率写出直线
的坐标和求出的斜率写出直线![]() 的方程,再由
的方程,再由![]() 与
与![]() 的坐标,利用两点间的距离公式求出
的坐标,利用两点间的距离公式求出![]() 即为弦心距,根据圆的半径,弦心距及弦的一半构成的直角三角形,利用勾股定理即可求出此时的弦长.
即为弦心距,根据圆的半径,弦心距及弦的一半构成的直角三角形,利用勾股定理即可求出此时的弦长.
解:(1)证明:因为![]() ,
,
所以![]() ,
,
因为![]() ,所以
,所以![]()
故直线![]() 过定点
过定点![]() .
.
因为圆![]() 的圆心为
的圆心为![]() ,
,![]() ,
,![]() ,则点
,则点![]() 在圆内.
在圆内.
所以直线![]() 与圆
与圆![]() 恒交于两点.
恒交于两点.
(2)由(1)知直线![]() 过定点
过定点![]() ,所以当直线
,所以当直线![]() 被圆
被圆![]() 截得的弦长最短时有
截得的弦长最短时有![]() ,
,
弦心距![]() ,
,
所以最短弦长为![]() .
.
因为![]() ,所以
,所以![]() ,故直线
,故直线![]() 的方程为
的方程为![]() .
.

 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
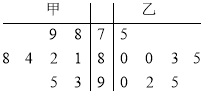
能考试全能100分系列答案【题目】某品牌经销商在一广场随机采访男性和女性用户各50名,其中每天玩微信超过6小时的用户列为“微信控”,否则称其为“非微信控”,调查结果如下:
微信控 | 非微信控 | 合计 | |
男性 | 26 | 24 | 50 |
女性 | 30 | 20 | 50 |
合计 | 56 | 44 | 100 |
(1)根据以上数据,能否有![]() 的把握认为“微信控”与“性别”有关?
的把握认为“微信控”与“性别”有关?
(2)现从调查的女性用户中按分层抽样的方法选出5人,再随机抽取3人赠送礼品,试求抽取3人中恰有2人是“微信控”的概率.
参考公式: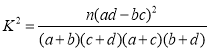 ,其中
,其中![]() .
.
参考数据:
| 0.050 | 0.040 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
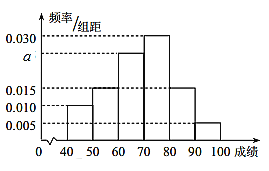
【题目】在某校举行的航天知识竞赛中,参与竞赛文科生与理科生人数之比为![]() ,且成绩分布在
,且成绩分布在![]() ,分数在80以上(含80)的同学获奖.按文理科用分层抽样的方法抽取200人的成绩作为样本,得到成绩的频率分布直方图如图所示.
,分数在80以上(含80)的同学获奖.按文理科用分层抽样的方法抽取200人的成绩作为样本,得到成绩的频率分布直方图如图所示.
文科生 | 理科生 | 合计 | |
获奖 | 5 | ||
不获奖 | |||
合计 | 200 |
参考公式: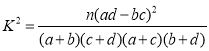 (其中
(其中![]() 为样本容量)
为样本容量)
随机变量![]() 的概率分布:
的概率分布:
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.001 | |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(1)求![]() 的值;
的值;
(2)填写上方的![]() 列联表,并判断能否有超过
列联表,并判断能否有超过![]() 的把握认为“获奖与学生的文、理科有关”?
的把握认为“获奖与学生的文、理科有关”?