Question

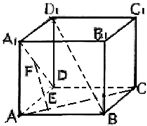如图所示，正方体ABCD-A₁B₁C₁D₁中，EF是异面直线，AC和A₁D的公垂线，则EF和BD₁的关系是（　　）

A．相交但不垂直

B．垂直

C．异面

D．平行

Answer 1

分析：建立以D₁为原点的空间直角坐标系D₁-xyz，设正方形的边长为1，利用向量法，我们易求出BD₁与A₁D和AC都垂直，根据共垂线的性质，可以得到两条线段平行．

解答：解：建立以D₁为原点的空间直角坐标系D₁-xyz，且设正方形的边长为1
所以就有D₁（0，0，0），B（1，1，0），A₁（1，0，0），D（0，0，1），A（1，0，1），C（0，1，1）
所以

A1D

=（-1，0，1），

AC

=（-1，1，0），

BD1

=（-1，-1，1）
所以

A1D

•

BD1

=-1+1=0 所以A₁D⊥BD₁，

AC

•

BD1

=1-1=0 所以AC⊥BD₁，
所以BD₁与A₁D和AC都垂直
又∵EF是AC、A₁D的公垂线，
∴BD₁∥EF
故选D

点评：本题考查空间中直线与直线之间的位置关系，其中建立空间坐标系，借助向量分析直线与直线之间的位置关系是解答本题的关键，这样降低了题目的难度，把纯理论的东西用数字的运算来解决．