题目内容
如图所示，正方体ABCD－A1B1C1D1中，E、F分别是AB、BC的中点，G为DD1上一点，且D1G：GD＝1：2，AC∩BD＝O，求证：平面AGO//平面D1EF．
|
同解析。
解析:
如答图所示，设EF∩BD＝H，在△DD1H中，
，
∴GO//D1H，又GO
平面D1EF，D1H
平面D1EF，
∴GO//平面D1EF，
在△BAO中，BE＝EF，BH＝HO，∴EH//AO
AO
平面D1EF，EH平面D1EF，∴AO//平面D1EF，
AO∩GO＝O，∴平面AGO//平面D1EF.
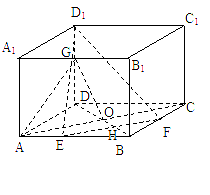
练习册系列答案
相关题目
如图所示，正方体ABCD-A1B1C1D1中，E、F分别是AB、BC的中点，G为DD1上一点，且D1G：GD=1：2，AC∩BD=O，求证：平面AGO∥平面D1EF．
如图所示，正方体ABCD-A1B1C1D1中，E、F分别是正方体ADD1A1和ABCD的中心，G是C1C的中点，设GF、C1F与AB所成的角分别为α、β，则α+β等于
如图所示，正方体ABCD－A1B1C1D1的棱长为1，点M在AB上，且AM＝
AB，点P在平面ABCD上，且动点P到直线A1D1的距离的平方与P到点M的距离的平方差为1，在平面直角坐标系xAy中，动点P的轨迹方程是________．