题目内容
5.已知函数f(x)=x2+2ax-3.(1)求实数a的取值范围,使得y=f(x)在区间[-4,6]上是单调函数;
(2)当x∈[-4,6]时,求f(x)的最小值g(a);
(3)画出分段函数g(x)图象,求g(x)的最大值.
分析 (1)求出函数的对称轴,要使f(x)在区间[-4,6]上是单调函数,则有-a≤-4或-a≥6;
(2)分类讨论,结合函数的单调性,求f(x)的最小值g(a);
(3)画出分段函数g(x)图象,即可求g(x)的最大值.
解答 解:(1)因为f(x)=x2+2ax-3=(x+a)2-3-a2,抛物线开口向上,且对称轴为x=-a.
要使f(x)在区间[-4,6]上是单调函数,则有-a≤-4或-a≥6,
解得a≥4或a≤-6;
(2)a≥4时,f(x)在区间[-4,6]上是单调增函数,f(x)的最小值g(a)=f(-4)=13-8a;
-6<a<4时,f(x)的最小值g(a)=f(-a)=-3-a2;
a≤-6时,f(x)在区间[-4,6]上是单调减函数,f(x)的最小值g(a)=f(6)=33+12a;
∴g(a)=$\left\{\begin{array}{l}{33+12a,a≤-6}\\{-3-{a}^{2},-6<a<4}\\{13-8a,a≥4}\end{array}\right.$;
(3)函数图象如图所示
g(x)的最大值是-3.
点评 本题考查函数的单调性与最小值,考查函数图象的作法,考查分类讨论的数学思想,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.命题p:?x∈R,函数f(x)=2cos2x+$\sqrt{3}$sin2x≤3,则( )
| A. | p是假命题;?p:?x0∈R,f(x0)=2cos2x0+$\sqrt{3}$sin2x0≤3 | |
| B. | p是假命题;?p:?x0∈R,f(x0)=2cos2x0+$\sqrt{3}$sin2x0>3 | |
| C. | p是真命题;?p:?x0∈R,f(x0)=2cos2x0+$\sqrt{3}$sin2x0≤3 | |
| D. | p是真命题;?p:?x0∈R,f(x0)=2cos2x0+$\sqrt{3}$sin2x0>3 |
13.一个空间几何体的三视图如图所示,则该几何体的外接球的表面积为( )
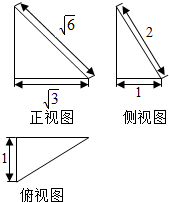

| A. | 5? | B. | 6? | C. | 2$\sqrt{7}$π | D. | 7π? |