题目内容
椭圆
中，以点
为中点的弦所在直线斜率为（ ）
中，以点为中点的弦所在直线斜率为（ ）A． |
B． |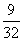
C． |
D． |
B
设弦AB的端点为
，则
，
,
两式相减得
又弦AB中点为
∴
，
即
∴
，则，,两式相减得
又弦AB中点为
∴
，即
∴
练习册系列答案
全能测控期末小状元系列答案
相关题目
全能测控期末小状元系列答案题目内容
中，以点为中点的弦所在直线斜率为（ ）| A． |
| B． |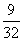
| C． |
| D． |
，则，,，全能测控期末小状元系列答案
的离心率为
，以原点为圆心、椭圆的短半轴长为半径的圆与直线
相切．
的方程；
，过点
作与
轴不重合的直线
交椭圆于
、
两点，连结
、
分别交直线
于
、
两点．试问直线
、
的斜率之积是否为定值，若是，求出该定值；若不是，请说明理由．
(a>b>0)的离心率为
，且椭圆C上一点与两个焦点F1，F2构成的三角形的周长为2
+2．
，若
，求
的取值范围．
的椭圆
上求一点Q，使该点到直线（
的距离最大。
过点
，且离心率
.
的直线
与该椭圆相交于A、B两点，试问：在直线
上是否存在点P，使得
是正三角形？若存在，求出点P的坐标；若不存在，请说明理由.
为焦点的椭圆上的一点,过焦点
作
的外角平分线的垂线,垂足为M点,则点M的轨迹是（ ）
的左焦点为
，直线
与椭圆相交于点
、
，当△FAB的周长最大时，
的面积是____________．
、
分别是椭圆
的左、右焦点，点
在椭圆
上，线段
的中点在
轴上，若
，则椭圆的离心率为（ ）
的左焦点，P是椭圆上一点，PF⊥x轴，OP∥AB(O为坐标原点)，则该椭圆的离心率是( )
