题目内容
实验北校举行运动会,组委会招墓了16名男志愿者和14名女志愿者,调查发现,男、女志愿者中分别有10 人和6人喜爱运动,其余不喜爱.
(1)根据以上数据完成以下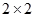 列联表:
列联表:
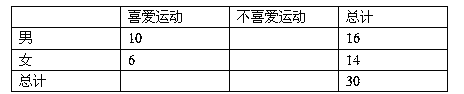
(2)根据列联表的独立性检验,有多大的把握认为性别与喜爱运动有关?
(3)从不喜爱运动的女志愿者中和喜爱运动的女志愿者中各选1人,求其中不喜爱运动的女生甲及喜爱运动的女生乙至少有一人被选取的概率.
参考公式 :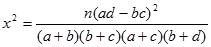 (其中
(其中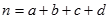 )
)
(1)根据以上数据完成以下
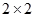 列联表:
列联表:
(2)根据列联表的独立性检验,有多大的把握认为性别与喜爱运动有关?
(3)从不喜爱运动的女志愿者中和喜爱运动的女志愿者中各选1人,求其中不喜爱运动的女生甲及喜爱运动的女生乙至少有一人被选取的概率.
参考公式 :
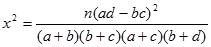 (其中
(其中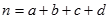 )
)| | 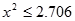 | 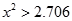 | 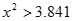 | 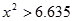 |
| 是否有关联 | 没有关联 | 90% | 95% | 99% |
(1)见解析;(2)性别与喜爱运动没有关联;(3)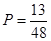 .
.
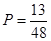 .
.试题分析:(1)独立性检验关键是计算出
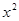 ,并同概率表作对比,选择适合的临界值
,并同概率表作对比,选择适合的临界值 ,得出是否具有相关性结论;(2)古典概型概率的计算,间接法:“1”减去既没有甲乙的概率.
,得出是否具有相关性结论;(2)古典概型概率的计算,间接法:“1”减去既没有甲乙的概率.试题解析:(1)由已知得:
| | 喜爱运动 | 不喜爱运动 | 总计 |
| 男 | 10 | 6 | 16 |
| 女 | 6 | 8 | 14 |
| 总计 | 16 | 14 | 30 |
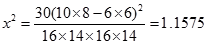 ,则:
,则: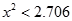 (选择第一个).
(选择第一个).则:性别与喜爱运动没有关联. 8分
(3)记不喜爱运动的女生甲及喜爱运动的女生乙至少有一人被选取为事件A,由已知得:从不喜爱运动的女志愿者中和喜爱运动的女志愿者中各抽取1人共有
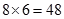 种方法,其中不喜爱运动的女生甲及喜爱运动的女生乙没有一人被选取的共有
种方法,其中不喜爱运动的女生甲及喜爱运动的女生乙没有一人被选取的共有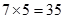 种方法,则:
种方法,则: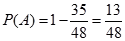 12分
12分
练习册系列答案
相关题目
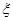 为取出的4个球中红球的个数,求
为取出的4个球中红球的个数,求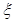 .
.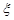 的数学期望和方差.
的数学期望和方差.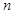 及天数如下表:
及天数如下表:

 .据以往资料统计,第一场比赛组织者可获得门票收入40万元,以后每场比赛门票收入比上一场增加10万元,则组织者在此次决赛中要获得的门票收入不少于390万元的概率为________.
.据以往资料统计,第一场比赛组织者可获得门票收入40万元,以后每场比赛门票收入比上一场增加10万元,则组织者在此次决赛中要获得的门票收入不少于390万元的概率为________.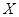 为选出的3名同学中女同学的人数,求随机变量
为选出的3名同学中女同学的人数,求随机变量