题目内容
有甲、乙两个班进行数学考试,按照大于或等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的2×2列联表:
已知从全部210人中随机抽取1人为优秀的概率为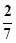 .
.
(1)请完成上面的2×2列联表;
(2)根据列联表的数据,若按99%的可靠性要求,能否认为“成绩与班级有关系”.
附: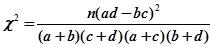 ,其中
,其中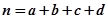 .
.
| | 优秀 | 非优秀 | 总计 |
| 甲班 | 20 | | |
| 乙班 | | 60 | |
| 总计 | | | 210 |
已知从全部210人中随机抽取1人为优秀的概率为
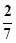 .
.(1)请完成上面的2×2列联表;
(2)根据列联表的数据,若按99%的可靠性要求,能否认为“成绩与班级有关系”.
附:
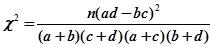 ,其中
,其中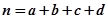 .
.| 参考数据 | 当 ≤2.706时,无充分证据判定变量A,B有关联,可以认为两变量无关联; ≤2.706时,无充分证据判定变量A,B有关联,可以认为两变量无关联; |
当 >2.706时,有90%的把握判定变量A,B有关联; >2.706时,有90%的把握判定变量A,B有关联; | |
当 >3.841时,有95%的把握判定变量A,B有关联; >3.841时,有95%的把握判定变量A,B有关联; | |
当 >6.635时,有99%的把握判定变量A,B有关联. >6.635时,有99%的把握判定变量A,B有关联. |
(1)
(2)有99%的把握认为“成绩与班级有关系”.
| | 优秀 | 非优秀 | 总计 |
| 甲班 | 20 | 90 | 110 |
| 乙班 | 40 | 60 | 100 |
| 总计 | 60 | 150 | 210 |
(2)有99%的把握认为“成绩与班级有关系”.
试题分析:(1)由于从全部210人中随机抽取1人为优秀的概率为
 ,可得优秀的人数=
,可得优秀的人数=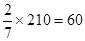 .即可得到乙班优秀的人数,甲班非优秀的人数;(2)假设
.即可得到乙班优秀的人数,甲班非优秀的人数;(2)假设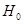 :“成绩与班级无关”.利用公式
:“成绩与班级无关”.利用公式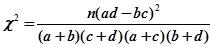 ,计算出
,计算出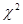 与
与 比较即可得出结论.
比较即可得出结论.试题解析:(1)由题意得甲、乙两个班级优秀人数之和为
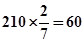 ,又甲班有20人,故乙班有40人.所以2×2列联表如下表所示:
,又甲班有20人,故乙班有40人.所以2×2列联表如下表所示:| | 优秀 | 非优秀 | 总计 |
| 甲班 | 20 | 90 | 110 |
| 乙班 | 40 | 60 | 100 |
| 总计 | 60 | 150 | 210 |
(2)假设
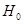 :“成绩与班级无关”.
:“成绩与班级无关”.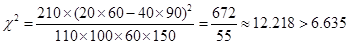
所以
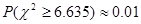 ,因此假设不成立.
,因此假设不成立.因此有99%的把握认为“成绩与班级有关系”.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
 及天数如下表:
及天数如下表: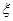 ,求
,求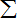
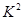 的一个可能取值为( )
的一个可能取值为( )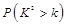
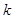
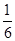
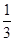
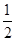
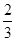
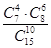 的是( )
的是( )