题目内容
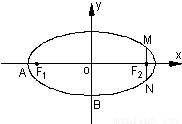
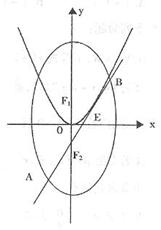
如图，椭圆C: 
的焦点为F1（0，c）、F2（0，一c）（c>0），抛物线
的焦点与F1重合，过F2的直线l与抛物线P相切，切点在第一象限，且与椭圆C相交于A、B两点，且
（I）求证：切线l的斜率为定值；
（Ⅱ）若抛物线P与直线l及y轴围成的图形面积为
，求抛物线P的方程；
（III）当
时，求椭圆离心率e的取值范围。
|
（Ⅰ）
（Ⅱ）
（III）
解析:
（I）依题意抛物线
设直线l与抛物线P的切点为
，又切点在第一象限，
则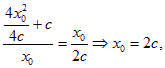
所以切线l的斜率
为定值。 ………………4分
（II）由（I）可得：
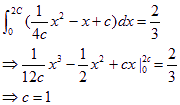
以抛物线P的方程为： ………………8分
（III）由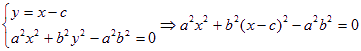
，
由
设
又
上单调递增，
练习册系列答案
相关题目
如图，在直角坐标系xOy中，已知椭圆C：
的离心率e＝
，
的离心率e＝
，左右两个焦分别为F1、F2．过右焦点F2且与x轴垂直的直线与椭圆C相交M、N两点，且|MN|＝1．
，(
)试求点P的轨迹方程，使点B关于该轨迹的对称点落在椭圆C上.
+
=1（a＞b＞0）的离心率e=
，左右两个焦分别为F1、F2．过右焦点F2且与轴垂直的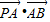
=m-4，（m∈R）试求点P的轨迹方程，使点B关于该轨迹的对称点落在椭圆C上．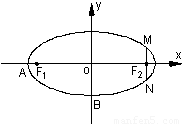
+
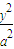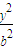=1（a＞b＞0）的离心率e=
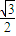，左右两个焦分别为F1、F2．过右焦点F2且与轴垂直的
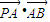=m-4，（m∈R）试求点P的轨迹方程，使点B关于该轨迹的对称点落在椭圆C上．