题目内容
3.已知向量$\overrightarrow a$=(2,-1),$\overrightarrow b$=(-1,m),$\overrightarrow c$=(-1,2),若($\overrightarrow a$+$\overrightarrow b$)∥$\overrightarrow c$,则m=-1;若($\overrightarrow a$+$\overrightarrow b$)⊥$\overrightarrow c$,则m=$\frac{3}{2}$.分析 由已知向量的坐标求出$\overrightarrow a$+$\overrightarrow b$的坐标,然后分别利用向量共线和斜率垂直的坐标表示列式求得m的值.
解答 解:∵$\overrightarrow a$=(2,-1),$\overrightarrow b$=(-1,m),∴$\overrightarrow{a}+\overrightarrow{b}=(1,m-1)$,
又$\overrightarrow c$=(-1,2),
由($\overrightarrow a$+$\overrightarrow b$)∥$\overrightarrow c$,得1×2-(m-1)×(-1)=0,解得:m=-1;
由($\overrightarrow a$+$\overrightarrow b$)⊥$\overrightarrow c$,得-1+2(m-1)=0,解得:m=$\frac{3}{2}$.
故答案为:-1;$\frac{3}{2}$.
点评 本题考查向量的数量积判断两个向量的垂直关系,考查计算能力,是基础题.

练习册系列答案
相关题目
14.函数y=sin($\frac{π}{3}$-2x)的单调减区间是( )
| A. | [2kπ-$\frac{π}{12}$,2kπ+$\frac{5π}{12}$](k∈Z) | B. | [kπ-$\frac{π}{12}$,kπ+$\frac{5π}{12}$](k∈Z) | ||
| C. | [2kπ+$\frac{5π}{12}$,2kπ+$\frac{11π}{12}$](k∈Z) | D. | [kπ+$\frac{5π}{12}$,kπ+$\frac{11π}{12}$](k∈Z) |
11.在△ABC中,$a=7,b=4\sqrt{3},c=\sqrt{13}$,则△ABC的最小角为( )
| A. | 60° | B. | 30° | C. | 15° | D. | 45° |
18.如图所示描述错误的是( )
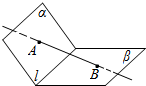

| A. | A∈α,B∈β | B. | α∩β=l | C. | AB∩α=A | D. | 直线AB与l相交 |