题目内容
在平面直角坐标系中,长度为3的线段AB的端点A、B分别在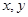 轴上滑动,点M在线段AB上,且
轴上滑动,点M在线段AB上,且 ,
,
(1)若点M的轨迹为曲线C,求其方程;
(2)过点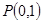 的直线
的直线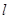 与曲线C交于不同两点E、F,N是曲线上不同于E、F的动点,求
与曲线C交于不同两点E、F,N是曲线上不同于E、F的动点,求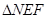 面积的最大值.
面积的最大值.
(1)C的方程是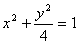 ;(2)
;(2)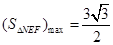 .
.
解析试题分析:(1)设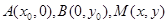 ,则
,则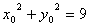 .用定比分点坐标公式可得
.用定比分点坐标公式可得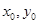 与
与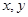 之间的关系式,将此关系式代入
之间的关系式,将此关系式代入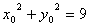 即得只含
即得只含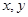 的方程,此即M的轨迹方程.(2)首先考虑直线的斜率不存在的情况,即
的方程,此即M的轨迹方程.(2)首先考虑直线的斜率不存在的情况,即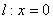 ,此时
,此时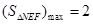 .当直线的斜率存在时,设
.当直线的斜率存在时,设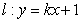 ,
,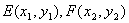 ,联立
,联立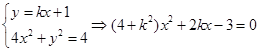 ,再用韦达定理即得
,再用韦达定理即得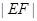 (含k的代数式).由题知过N的直线
(含k的代数式).由题知过N的直线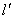
 ,且
,且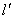 与椭圆切于N点时,
与椭圆切于N点时,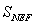 最大,故设
最大,故设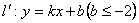
联立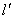 与椭圆方程得
与椭圆方程得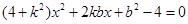 ,此时
,此时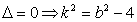 .
.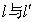 的距离
的距离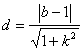 即为点N到EF的距离,所以
即为点N到EF的距离,所以

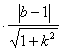 ,化简
,化简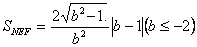 ,平方后利用导数可得其最大值.
,平方后利用导数可得其最大值.
(1)由题知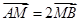 ,设
,设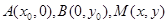
有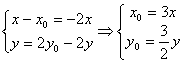 代入
代入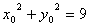 得
得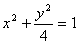 ,
,
所以曲线C的方程是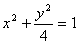 4分
4分
(2)当直线的斜率不存在时,即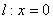 ,此时
,此时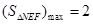 5分
5分
当直线的斜率存在时,设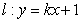 ,
,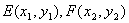
联立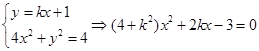 ,有
,有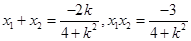 .
.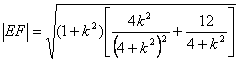 7分
7分
由题知过N的直线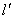
 ,且
,且 与椭圆切于N点时,
与椭圆切于N点时,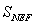 最大,故设
最大,故设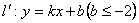
联立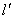 与椭圆方程得
与椭圆方程得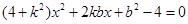 ,此时
,此时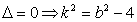
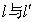 的距离
的距离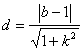 ,所以
,所以

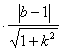
化简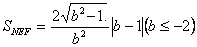 10分
10分
设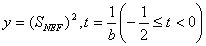 ,有
,有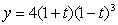
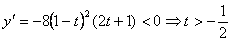 ,所以函数
,所以函数 在
在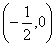 上单调递减,当
上单调递减,当 时,函数
时,函数 取得最大值
取得最大值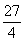 ,即
,即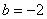 时
时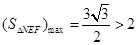
综上所述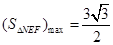 .13分.
.13分.
考点:1、轨迹方程的求法;2、直线与圆锥曲线的关系;3、利用导数求最值.

练习册系列答案
相关题目
 ,其中
,其中
 在其定义域上的单调性;
在其定义域上的单调性; 时,求
时,求 的值.
的值. 在
在 处取得极值-2.
处取得极值-2. 的解析式;
的解析式;  在点
在点 处的切线方程.
处的切线方程. .
. 在
在 时有极值,求实数
时有极值,求实数 的值和
的值和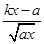 -ln a(x>0,a>0且为常数).
-ln a(x>0,a>0且为常数).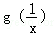 的大小关系;
的大小关系; 对任意x>0成立.
对任意x>0成立.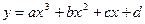 满足下列条件:
满足下列条件: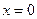 处导数为-1;③在
处导数为-1;③在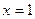 处切线方程为
处切线方程为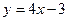 .
.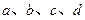 的值;
的值;