题目内容
（本题满分14分）已知椭圆C的中心在原点，焦点
、
在x轴上，点P为椭圆上的一个动点，且
的最大值为90°，直线l过左焦点与椭圆交于A、B两点，
△
的面积最大值为12．
（1）求椭圆C的离心率；（5分）
（2）求椭圆C的方程。（9分）
（本题满分14分）
解：（1）根据椭圆的定义，可知动点
的轨迹为椭圆，设椭圆方程：
其焦距为
， 则 
，
，则
．
所以动点M的轨迹方程为：
． ………………………5分
（2）当直线
的斜率不存在时，不满足题意．
当直线的斜率存在时，设直线的方程为
，设
，
，
∵
，∴
． ………………………6分
∵
，
， ∴
．
∴ 
．（1） ………………………8分
由方程组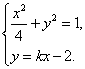
得． 
由
得 
则
，
， ………………………11分
代入①，得
．
即
，解得，
或
． 经验证
。 ………………………13分
所以，直线的方程是
或
． ………………………14分
练习册系列答案
相关题目
，
，函数
. （Ⅰ）求
的单调增区间； （II）若在
中，角
所对的边分别是
，且满足：
，求
的取值范围.
，且以下命题都为真命题：
实系数一元二次方程
的两根都是虚数；
存在复数
同时满足
且
.
的取值范围.
，求x的值；
对于
恒成立，求实数m的取值范围. 
：
的离心率为
，过坐标原点
且斜率为
的直线
与
、
，
．
、
的值；
与椭圆
的取值范围．
，AB=BC=2AD=4，E、F分别是AB、CD上的点，EF∥BC，AE = x，G是BC的中点．沿EF将梯形ABCD翻折，使平面AEFD⊥平面EBCF
（如图）.
，
