题目内容
【题目】已知数列![]() 满足
满足![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)对任意给定的![]() ,是否存在
,是否存在![]() (
(![]() )使
)使![]() 成等差数列?若存
成等差数列?若存
在,用![]() 分别表示
分别表示![]() 和
和![]() (只要写出一组);若不存在,请说明理由;
(只要写出一组);若不存在,请说明理由;
(3)证明:存在无穷多个三边成等比数列且互不相似的三角形,其边长为![]() .
.
【答案】(1)![]() ; (2)当
; (2)当![]() 时,不存在p,r;当
时,不存在p,r;当![]() 时,存在
时,存在![]() 满足题设;(3)证明见解析.
满足题设;(3)证明见解析.
【解析】
(1)由![]() 可求出数列
可求出数列![]() 的通项公式;(2)分
的通项公式;(2)分![]() 和
和![]() 两种情况讨论,根据题中条件求出
两种情况讨论,根据题中条件求出![]() ,
,![]() ,
,![]() 的大小关系,再设
的大小关系,再设![]() ,即可用
,即可用![]() 表示
表示![]() 和
和![]() ;(3)构造三角形三边分别为
;(3)构造三角形三边分别为![]() ,
,![]() ,
,![]() ,然后用反证法证明任意两个三角形互不相似,本题得证
,然后用反证法证明任意两个三角形互不相似,本题得证
(1)当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,
,
所以![]() ;
;
综上所述,![]() .
.
(2)当![]() 时,若存在p,r使
时,若存在p,r使![]() 成等差数列,则
成等差数列,则![]() ,
,
因为![]() ,所以
,所以![]() ,与数列
,与数列![]() 为正数相矛盾,因此,当
为正数相矛盾,因此,当![]() 时不存在;
时不存在;
当![]() 时,设
时,设![]() ,则
,则![]() ,所以
,所以![]() ,
,
令![]() ,得
,得![]() ,此时
,此时![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
所以![]() ;
;
综上所述,当![]() 时,不存在p,r;当
时,不存在p,r;当![]() 时,存在
时,存在![]() 满足题设.
满足题设.
(3)作如下构造:![]() ,其中
,其中![]() ,
,
它们依次为数列![]() 中的第
中的第![]() 项,第
项,第![]() 项,第
项,第![]() 项,
项,
显然它们成等比数列,且![]() ,
,![]() ,所以它们能组成三角形.
,所以它们能组成三角形.
由![]() 的任意性,这样的三角形有无穷多个.
的任意性,这样的三角形有无穷多个.
下面用反证法证明其中任意两个三角形![]() 和
和![]() 不相似:
不相似:
若三角形![]() 和
和![]() 相似,且
相似,且![]() ,则
,则![]() ,
,
整理得![]() ,所以
,所以![]() ,这与条件
,这与条件![]() 相矛盾,
相矛盾,
因此,任意两个三角形不相似.故命题成立.

【题目】假设某种设备使用的年限![]() (年)与所支出的维修费用
(年)与所支出的维修费用![]() (万元)有以下统计资料:
(万元)有以下统计资料:
使用年限 | 2 | 3 | 4 | 5 | 6 |
维修费用 | 2 | 4 | 5 | 6 | 7 |
若由资料知![]() 对
对![]() 呈线性相关关系.试求:
呈线性相关关系.试求:
(1)求![]() ;
;
(2)线性回归方程![]() ;
;
(3)估计使用10年时,维修费用是多少?
附:利用“最小二乘法”计算![]() 的值时,可根据以下公式:
的值时,可根据以下公式: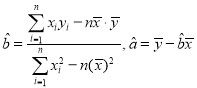
【题目】2019年6月13日,三届奥运亚军,羽坛传奇,马来西亚名将李宗伟宣布退役,当天有大量网友关注此事件,某网上论坛从关注此事件跟帖中,随机抽取了100名网友进行调查统计,先分别统计他们在跟帖中的留言条数,再把网友人数按留言条数分成6组;![]()
![]()
![]()
![]()
![]()
![]() ,得到如下图所小的频率分布直方图;并将其中留言不低于40条的规定为“强烈关注”,否则为“一般关注”,对这100名网友进一步统计,得到部分数据如下的列联表.
,得到如下图所小的频率分布直方图;并将其中留言不低于40条的规定为“强烈关注”,否则为“一般关注”,对这100名网友进一步统计,得到部分数据如下的列联表.
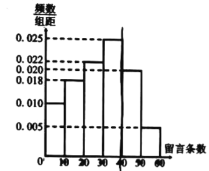

(1)在答题卡上补全2×2列联表中数据,并判断能否有95%的把握认为网友对此事件是否为“强烈关注”与性别有关?
(2)该论坛欲在上述“强烈关注”的网友中按性别进行分层抽样,共抽取5人,并在此5人中随机抽取两名接受访谈,记女性访谈者的人数为占,求5的分布列与数学期望.
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
参考公式与数据: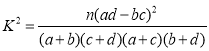 ,其中
,其中![]() .
.
