题目内容
如图，已知边长都为1正方形ABCD与正方形ABEF，∠DAF=90°，M，N分别是对角线AC和BF上的点，且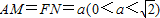
．（1）求证：MN∥平面BCE；
（2）求MN的最小值．
【答案】分析：（1）过M作MP⊥AB，垂足为P，连接PN，由平行线分线段成比例定理，我们易得到PN∥AF，由面面平行的判定定理可得平面MPN∥平面CBE，再由面面平行的性质，即可得到MN∥平面BCE；
（2）由已知中边长都为1正方形ABCD与正方形ABEF，∠DAF=90°，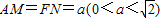
，根据勾股定理，我们易得MN2=
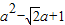，根据二次函数的性质，易得到MN的最小值．
解答：解：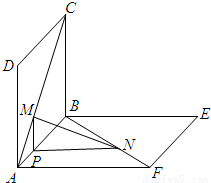
（1）证明：过M作MP⊥AB，垂足为P，连接PN．
∵
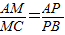，又
∴
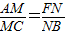
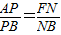[（2分）]
∴PN∥AF
∴平面MPN∥平面CBE[（4分）]
从而MN∥平面BCE[（6分）]
（2）∠MPN=90°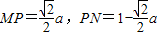
[（8分）]
由勾股定理知：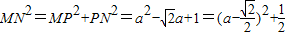
[（10分）]
当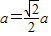
时，MN的最小值为
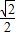．[（12分）]
点评：本题考查的知识点是直线与平面平行的判定，空间中两点之间的距离运算，其中（1）中，根据线面平行的判定定理证明有较大的难度，故采用先证面面平行，再由面面平行的性质得到线面平行，（2）的关键是将空间两点间的距离表示成a的函数，进而转化成求函数最值的问题．
（2）由已知中边长都为1正方形ABCD与正方形ABEF，∠DAF=90°，
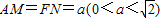，根据勾股定理，我们易得MN2=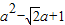，根据二次函数的性质，易得到MN的最小值．解答：解：
（1）证明：过M作MP⊥AB，垂足为P，连接PN．∵
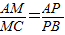，又∴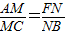
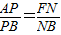[（2分）]∴PN∥AF
∴平面MPN∥平面CBE[（4分）]
从而MN∥平面BCE[（6分）]
（2）∠MPN=90°
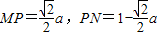[（8分）]由勾股定理知：
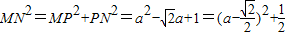[（10分）]当
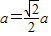时，MN的最小值为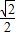．[（12分）]点评：本题考查的知识点是直线与平面平行的判定，空间中两点之间的距离运算，其中（1）中，根据线面平行的判定定理证明有较大的难度，故采用先证面面平行，再由面面平行的性质得到线面平行，（2）的关键是将空间两点间的距离表示成a的函数，进而转化成求函数最值的问题．
练习册系列答案
相关题目
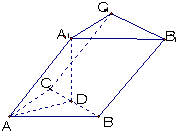如图，已知三棱柱ABC-A1B1C1的侧棱长与底面边长都等于1，A1在底面ABC上的射影D为BC的中点，则侧棱AA1与底面ABC所成角的大小为
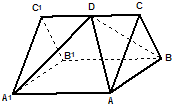（2013•松江区二模）如图，已知ABC-A1B1C1是正三棱柱，它的底面边长和侧棱长都是2，D为侧棱CC1的中点．
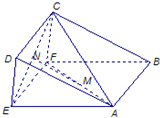（2013•揭阳二模）如图，已知三棱柱BCF-ADE的侧面CFED与ABFE都是边长为1的正方形，M、N两点分别在AF和CE上，且AM=EN．