题目内容
已知函数f(x)=2x-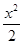 -aln(x+1),a∈R.
-aln(x+1),a∈R.
(1)若a=-4,求函数f(x)的单调区间;
(2)求y=f(x)的极值点(即函数取到极值时点的横坐标).
(1)f(x)的单调增区间为(-1,3), 单调减区间为(3,+∞)。
(2)
ⅰ.  7分
7分
ⅱ.当 时,若
时,若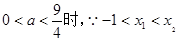 ,由函数的单调性可知f(x)有极小值点
,由函数的单调性可知f(x)有极小值点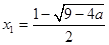 ;有极大值点
;有极大值点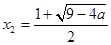 。若
。若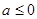 时, f(x)有极大值点
时, f(x)有极大值点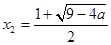 ,无极小值点。
,无极小值点。
解析试题分析:(1)因为,f(x)=2x-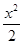 -aln(x+1),a∈R,定义域为(-1,+∞)。
-aln(x+1),a∈R,定义域为(-1,+∞)。
所以,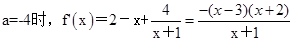 ,
,
故,f(x)的单调增区间为(-1,3), 单调减区间为(3,+∞)。
(2)因为,f(x)=2x-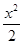 -aln(x+1),a∈R,定义域为(-1,+∞)。
-aln(x+1),a∈R,定义域为(-1,+∞)。
所以, ,
, =0有实根的条件是
=0有实根的条件是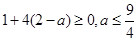 。
。
ⅰ. 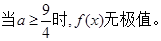
ⅱ.当 时,若
时,若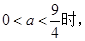 f(x)有极小值点
f(x)有极小值点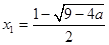 ;有极大值点
;有极大值点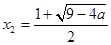 。若
。若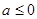 时, f(x)有极大值点
时, f(x)有极大值点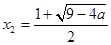 ,无极小值点。
,无极小值点。
考点:应用导数研究函数的单调性、极值。
点评:中档题,研究函数的单调性、极值、最值等,是导数应用的基本问题。求函数的单调区间,主要研究导函数非负,确定增区间;利用导函数值非正,确定减区间。求函数的极值,遵循“求导数,求驻点,研究单调性,求极值”。本题(2)需要对a进行分类讨论,易出错。

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
 ,
, ,
, (1)若
(1)若 ,求函数
,求函数 的极值;
的极值; 在
在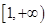 上单调递减,求实数
上单调递减,求实数 的取值范围;
的取值范围; 的图象上是否存在不同的两点
的图象上是否存在不同的两点 ,使线段
,使线段 的中点的横坐标
的中点的横坐标 与直线
与直线 之间满足
之间满足 ?若存在,求出
?若存在,求出
 时,讨论
时,讨论 的单调性;
的单调性; 时,
时, ,求
,求 的取值范围.
的取值范围.
 ,求函数
,求函数 的极小值;
的极小值; ,试问:在定义域内是否存在三个不同的自变量
,试问:在定义域内是否存在三个不同的自变量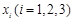 使得
使得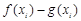 的值相等,若存在,请求出
的值相等,若存在,请求出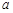 的范围,若不存在,请说明理由?
的范围,若不存在,请说明理由?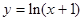
 ,证明
,证明 ;
; 时
时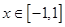 和
和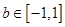 都恒成立,求实数
都恒成立,求实数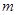 的取值范围。
的取值范围。
 .
. 在点
在点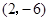 处的切线方程;
处的切线方程; 为曲线
为曲线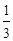 x3-
x3-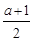 x2+a x.
x2+a x.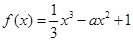
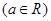 .
.