题目内容
在棱长为1的正方体ABCD-A1B1C1D1中，M是AC的中点，点P在正方体的表面上运动，则总能使B1C与MP垂直的点P所构成的轨迹的周长等于________．
分析：分别取BC，CC1，DD1，AD的中点O，N，R，S，则使B1C与MP垂直的点P所构成的轨迹为矩形ONRS，由此可得使B1C与MP垂直的点P所构成的轨迹的周长．
解答：
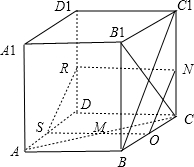解：分别取BC，CC1，DD1，AD的中点O，N，R，S，则ON∥BC1，OS∥CD∵B1C⊥BC1，∴B1C⊥ON
∵B1C⊥OS，OS∩ON=O
∴B1C⊥平面ONRS
∴使B1C与MP垂直的点P所构成的轨迹为矩形ONRS
∵正方体的棱长为1
∴使B1C与MP垂直的点P所构成的轨迹的周长等于
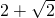
故答案为：
点评：本题考查立体几何中的轨迹问题，考查学生的分析解决问题的能力，解题的关键是确定使B1C与MP垂直的点P所构成的轨迹．
练习册系列答案
名师指导期末冲刺卷系列答案
相关题目
在线段AD1上运动，给出以下四个命题：
在棱长为1的正方体ABCD-A1B1C1D1中，M和N分别为A1B1 和BB1的中点，那么直线AM与CN所成角的余弦值是（ ）
（理科）如图，在棱长为1的正方体A'C中，过BD及B'C'的中点E作截面BEFD交C'D'于F．
（2004•武汉模拟）（文科）在棱长为1的正方体ABCD-A′B′C′D′中，AC′为对角线，M、N分别为BB′，B′C′中点，P为线段MN中点．