题目内容
过点P(3,0)作一直线,使它夹在两直线l1:2x-y-2=0与l2:x+y+3=0之间的线段AB恰被点P平分,求此直线的方程.
所求的直线方程为8x-y-24=0
方法一 设点A(x,y)在l1上,
由题意知 ,∴点B(6-x,-y),
,∴点B(6-x,-y),
解方程组 ,
,
得 ,∴k=
,∴k=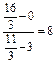 .
.
∴所求的直线方程为y=8(x-3),
即8x-y-24=0.
方法二 设所求的直线方程为y=k(x-3),
则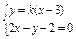 ,解得
,解得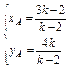 ,
,
由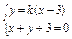 ,解得
,解得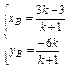 .
.
∵P(3,0)是线段AB的中点,
∴yA+yB=0,即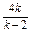 +
+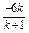 =0,
=0,
∴k2-8k=0,解得k=0或k=8.
又∵当k=0时,xA=1,xB=-3,
此时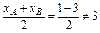 ,∴k=0舍去,
,∴k=0舍去,
∴所求的直线方程为y=8(x-3),
即8x-y-24=0.
由题意知
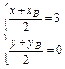 ,∴点B(6-x,-y),
,∴点B(6-x,-y),解方程组
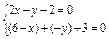 ,
,得
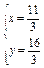 ,∴k=
,∴k=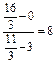 .
.∴所求的直线方程为y=8(x-3),
即8x-y-24=0.
方法二 设所求的直线方程为y=k(x-3),
则
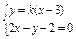 ,解得
,解得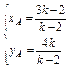 ,
,由
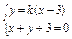 ,解得
,解得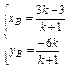 .
.∵P(3,0)是线段AB的中点,
∴yA+yB=0,即
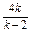 +
+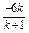 =0,
=0,∴k2-8k=0,解得k=0或k=8.
又∵当k=0时,xA=1,xB=-3,
此时
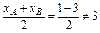 ,∴k=0舍去,
,∴k=0舍去,∴所求的直线方程为y=8(x-3),
即8x-y-24=0.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
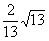
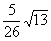
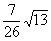
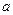 满足什么条件时,
满足什么条件时,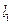 :
: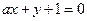 ,
,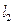 :
: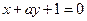 ,
,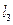 :
: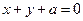 三条直线只有两个交点?
三条直线只有两个交点?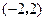 的直线与两条坐标轴围成的三角形的面积等于12,
的直线与两条坐标轴围成的三角形的面积等于12,