题目内容
已知正项等差数列{an}的前20项和为100,则a5•a16的最大值是
- A.100
- B.75
- C.25
- D.50
C
分析:设出等差数列的通项公式和前n项和公式分别为an=a+(n-1)d,sn=na+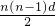 ,由前20项和为100得到2a+19d=10,而a5+a16=(a+4d)+(a+15d)=2a+19d=10,所以利用基本不等式a+b≥2
,由前20项和为100得到2a+19d=10,而a5+a16=(a+4d)+(a+15d)=2a+19d=10,所以利用基本不等式a+b≥2  当且仅当a=b时取等号,且a,b为正数,得到a5•a16的最大值即可.
当且仅当a=b时取等号,且a,b为正数,得到a5•a16的最大值即可.
解答:设等差数列首项为a,公差为d,则an=a+(n-1)d,sn=na+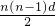 ,
,
因为前20项和为100得s20=20a+190d=100即2a+19d=10
所以a5+a16=(a+4d)+(a+15d)=2a+19d=10,
因为各项为正,所以a5+a16≥2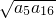 即a5•a16≤
即a5•a16≤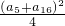 =25
=25
所以a5•a16的最大值为25
故选C
点评:本题考查等差数列的性质,这种题目的运算量比较小,是一个简单的综合题目,题目中涉及到的基本不等式平时用的比较多,这种结合希望引起同学们注意.
分析:设出等差数列的通项公式和前n项和公式分别为an=a+(n-1)d,sn=na+
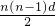 ,由前20项和为100得到2a+19d=10,而a5+a16=(a+4d)+(a+15d)=2a+19d=10,所以利用基本不等式a+b≥2
,由前20项和为100得到2a+19d=10,而a5+a16=(a+4d)+(a+15d)=2a+19d=10,所以利用基本不等式a+b≥2  当且仅当a=b时取等号,且a,b为正数,得到a5•a16的最大值即可.
当且仅当a=b时取等号,且a,b为正数,得到a5•a16的最大值即可.解答:设等差数列首项为a,公差为d,则an=a+(n-1)d,sn=na+
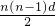 ,
,因为前20项和为100得s20=20a+190d=100即2a+19d=10
所以a5+a16=(a+4d)+(a+15d)=2a+19d=10,
因为各项为正,所以a5+a16≥2
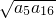 即a5•a16≤
即a5•a16≤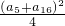 =25
=25所以a5•a16的最大值为25
故选C
点评:本题考查等差数列的性质,这种题目的运算量比较小,是一个简单的综合题目,题目中涉及到的基本不等式平时用的比较多,这种结合希望引起同学们注意.

练习册系列答案
相关题目
已知正项等差数列{an}的前20项和为100,则a5•a16的最大值是( )
| A、100 | B、75 | C、25 | D、50 |
已知正项等差数列{an}的前20项的和为100,那么a7a14的最大值为( )
| A、75 | B、100 | C、50 | D、25 |