Question

（本题满分15分）

已知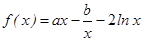，且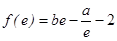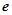（为自然对数的底数）。

（1）求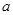与的关系；

（2）若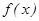在其定义域内为增函数，求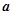的取值范围；

（3）证明：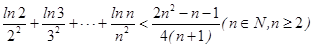

(提示：需要时可利用恒等式：)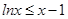

 

Answer 1

【答案】

解：（1）由题意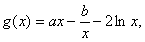

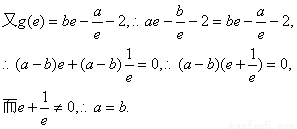
   （2）由（1）知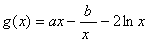：（x>0）

令h(x)=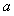x²－2x+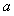.要使g(x)在（0，+∞）为增函数，只需h(x)在（0，+∞）满足：

h(x)≥0恒成立.

即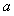x²－2x+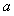≥0

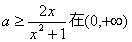上恒成立[来源:ZXXK][来源:学,科,网Z,X,X,K]

又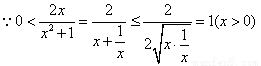

所以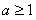

   （3）证明：证：lnx－x+1≤0  (x>0)，

设.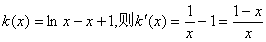

当x∈（0，1）时，k′(x)>0，∴k(x)为单调递增函数；

当x∈（1，∞）时，k′(x)<0，∴k(x)为单调递减函数；

∴x=1为k(x)的极大值点，

∴k(x)≤k(1)=0.

即lnx－x+1≤0，∴lnx≤x－1.

②由①知lnx≤x－1,又x>0，

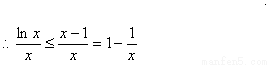
【解析】略