题目内容
a11，a12，……a18
a21，a22，……a28
……………………
64个正数排成8行8列, 如下所示： a81，a82，……a88
在符合
中，i表示该数所在的行数，j表示该数所在的列数。已知每一行中的数依次都成等差数列，而每一列中的数依次都成等比数列（每列公比q都相等）且
，
，
。
⑴若
，求
和
的值。
⑵记第n行各项之和为An（1≤n≤8），数列{an}、{bn}、{cn}满足
，联
（m为非零常数），
，且
，求
的取值范围。
⑶对⑵中的
，记
，设
，求数列
中最大项的项数。
（1）
（2）
（3）
中最大项的项数为7项.
解析:
⑴∵
， ∴
∵
成等差 ∴
⑵设第一行公差为d，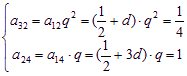 
解出：
，
′
∵
∴
∴
∵
∴
而
∴
∴
是等差数列
故
∵
∴
∴
⑶∵
是一个正项递减数列
∴
，
∴中最大项满足
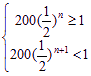
解出：6.643<n≤7.643
∵
, ∴n=7，即中最大项的项数为7项.
练习册系列答案
相关题目