题目内容
n2(n≥4)个正数排成如右表所示的n行n列:
,其中第一行从左到右成等差数列,每一列从上到下成等比数列,且公比均相等.若已知a42=
,a43=
,a24=2,则a11+a22+a33+…+ann=
|
| 1 |
| 4 |
| 3 |
| 8 |
4-
| 4+2n |
| 2n |
4-
.| 4+2n |
| 2n |
分析:设出a11,第一行数的公差,第一列数的公比,求出表中通项ast,据通项及条件,即可求得首项、公差、公比,进而可求出akk,再利用错位相减法求出数列的和.
解答:解:设a11=a,第一行数的公差为d,第一列数的公比为q,可得ast=[a+(t-1)d]qs-1,第四行数列公差是dq3,
于是可得 a24=(a11+3d)q=2,a42=(a11+d)q3=
,a43=a42+dq3=
,解得a11=d=1,q=
,
于是对任意的1≤k≤n,有akk=a1kqk-1=[a11+(k-1)d]qk-1=
∴S=
+
+…+
又
S=
+
+…+
两式相减后得:
S=1+
+…+
-
∴S=4-
.
于是可得 a24=(a11+3d)q=2,a42=(a11+d)q3=
| 1 |
| 4 |
| 3 |
| 8 |
| 1 |
| 2 |
于是对任意的1≤k≤n,有akk=a1kqk-1=[a11+(k-1)d]qk-1=
| k |
| 2k-1 |
∴S=
| 1 |
| 20 |
| 2 |
| 21 |
| n |
| 2n-1 |
又
| 1 |
| 2 |
| 1 |
| 21 |
| 2 |
| 22 |
| n |
| 2n |
两式相减后得:
| 1 |
| 2 |
| 1 |
| 21 |
| 1 |
| 2n-1 |
| n |
| 2n |
∴S=4-
| 4+2n |
| 2n |
点评:本题考查归纳推理,考查求数列的前n项和,数列的通项,根据数列通项的特点选择合适的求和方法是关键.

练习册系列答案
相关题目
 如图,n2(n≥4)个正数排成n行n列方阵:符号aij(1≤i,j≤n)表示位于第i行第j列的正数.已知每一行的数成等差数列,每一列的数成等比数列,且各列数的公比都等于q.若
如图,n2(n≥4)个正数排成n行n列方阵:符号aij(1≤i,j≤n)表示位于第i行第j列的正数.已知每一行的数成等差数列,每一列的数成等比数列,且各列数的公比都等于q.若 n2(n≥4)个正数排成n行n列:其中每一行的数由左至右成等差数列,每一列的数由上至下成等比数列,并且所有公比相等,已知a24=1,
n2(n≥4)个正数排成n行n列:其中每一行的数由左至右成等差数列,每一列的数由上至下成等比数列,并且所有公比相等,已知a24=1,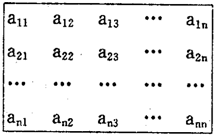 (2012•洛阳一模)如图,n2(n≥4)个正数排成n×n方阵,aij(1≤i,j≤n)表示位于第i行第j列的正数.已知每一行的数成等差数列,每一列的数成等比数列,且每一列数的公比都等于q.若a11=1,a23=1,a32=
(2012•洛阳一模)如图,n2(n≥4)个正数排成n×n方阵,aij(1≤i,j≤n)表示位于第i行第j列的正数.已知每一行的数成等差数列,每一列的数成等比数列,且每一列数的公比都等于q.若a11=1,a23=1,a32=