题目内容
|
(Ⅰ) (Ⅱ) (Ⅲ)
解析:
法一:
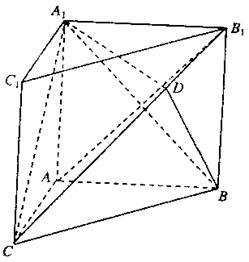
(I)由AC=1,AB=![]() ,BC=
,BC=![]() 知AC2+AB2=BC2,
知AC2+AB2=BC2,
所以AC⊥AB。
因为ABC—A1B1C1是直三棱柱,面ABB1A1⊥面ABC,
所以AC⊥面ABB1A1。………………3分
由![]() ,知侧面ABB1A1是正方形,连结AB1,
,知侧面ABB1A1是正方形,连结AB1,
所以A1B⊥AB1。
由三垂线定理得A1B⊥B1C。 ………………6分
(II)作BD⊥B1C,垂足为D,连结A1D。
由(I)知,A1B⊥B1C,则B1C⊥面A1BD,
于是B1C⊥A1D,
则∠A1DB为二面角
A1—B1C—B的平面角。 ………………8分
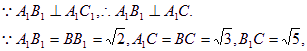
∴Rt△A1B1C≌Rt△B1BC,
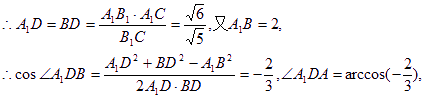
故二面角A1—B1C—B的大小为![]() ………………12分
………………12分
|
解法二:由AC=1,AB=![]() ,BC=
,BC=![]() 知AC2+AB2=BC2,所以AC⊥AB。
知AC2+AB2=BC2,所以AC⊥AB。
如图建立空间直角坐标系![]()
![]()
![]() …2分
…2分
(I)![]() ,
,
![]() ……6分
……6分
(II)作![]() ,垂足为D,连结A1D。
,垂足为D,连结A1D。
设![]()
![]() ,
,
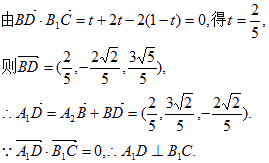
所以![]() 等于二面角A1—B1C—B的大小。 ………………10分
等于二面角A1—B1C—B的大小。 ………………10分
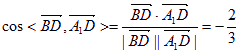 ,故二面角A1—B1C—B的大小为
,故二面角A1—B1C—B的大小为![]() ……12分
……12分

练习册系列答案
相关题目

 两点有5条连线并联,它们在单位时间内能通过的信息量依次为
两点有5条连线并联,它们在单位时间内能通过的信息量依次为 .现从中任取三条线且记在单位时间内通过的信息总量为
.现从中任取三条线且记在单位时间内通过的信息总量为 .
.
 ∩平面
∩平面 =AB,PQ⊥
=AB,PQ⊥
 .
.
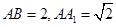 ,求点
,求点 到平面
到平面 的距离;
的距离;
 为何值时,二面角
为何值时,二面角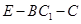 的正弦值为
的正弦值为 ?
? ,求证:MN ⊥平面PCD.
,求证:MN ⊥平面PCD.