题目内容
如图,在△
 中,
中, ,
, 为
为 中点,
中点, .记锐角
.记锐角 .且满足
.且满足 .
.
(1)求
 ;
; (2)求
 边上高的值.
边上高的值.(1)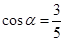 (2)
(2)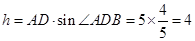
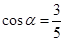 (2)
(2)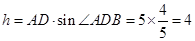
试题分析:(1)∵
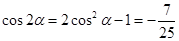 ,∴
,∴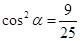 ,
,∵
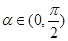 ,∴
,∴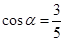 . -6分
. -6分(2)方法一、由(1)得
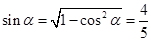 ,
, ∵
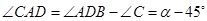 , 7
, 7∴
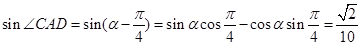 , -10分
, -10分在
 中,由正弦定理得:
中,由正弦定理得: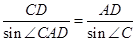 ,
,∴
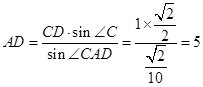 , - 12分
, - 12分则高
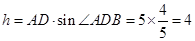 . -13分
. -13分方法二、如图,作
 边上的高为
边上的高为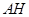
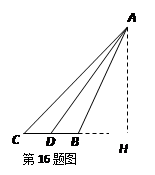
在直角△
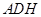 中,由(1)可得
中,由(1)可得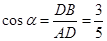 ,
,则不妨设
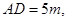 则
则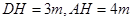 9分
9分注意到
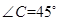 ,则
,则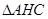 为等腰直角三角形,所以
为等腰直角三角形,所以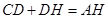 ,
,则
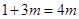 -11分
-11分所以
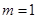 ,即
,即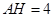 13分
13分点评:解决的关键是利用三角函数值来表示边和长度,进而结合三角形的性质来得到求解。属于基础题。

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目

 ,函数
,函数
 的最小正周期;
的最小正周期; 分别为△ABC内角A,B,C的对边,
分别为△ABC内角A,B,C的对边, ,且
,且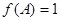 ,求A和△ABC面积的最大值。
,求A和△ABC面积的最大值。 中,
中, 为角
为角 所对的边,且
所对的边,且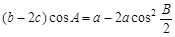 。
。 的值; (2)若
的值; (2)若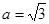 ,则求
,则求 的取值范围。
的取值范围。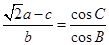 ,则B的大小为 .
,则B的大小为 . ABC中,
ABC中, 所对边分别为
所对边分别为 ,且满足
,且满足


 的值;
的值; 的值.
的值.  中,
中, ,则A的取值范围是 .
,则A的取值范围是 . ,向量
,向量
 ,且满足
,且满足 。
。 ,求角
,求角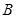 ;
; ,△ABC的面积
,△ABC的面积 ,求△ABC的周长。
,求△ABC的周长。 点出发,甲以每小时
点出发,甲以每小时 的速度向正东航行,乙船以每小时
的速度向正东航行,乙船以每小时 的速度沿南偏东
的速度沿南偏东 的方向航行,
的方向航行, 小时后,甲、乙两船分别到达
小时后,甲、乙两船分别到达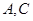 两点,此时
两点,此时 的大小为 ;
的大小为 ; 的两根,则这个直角三角形的斜边长等于( )
的两根,则这个直角三角形的斜边长等于( )