题目内容
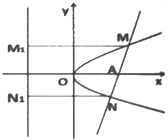 过抛物线y2=2Px(P>0)的对称轴上一点A(a,0)(a>0)的直线与抛物线相交于M,N两点,自M,N向直线l:x=-a作垂线,垂足分别为M1,N1.
过抛物线y2=2Px(P>0)的对称轴上一点A(a,0)(a>0)的直线与抛物线相交于M,N两点,自M,N向直线l:x=-a作垂线,垂足分别为M1,N1.(1)当a=
| P | 2 |
(2)记△AMM1,△AM1N1,△ANN1的面积分别为S1,S2,S3,是否存在λ,使得对任意的a>0,均有 S22=λS1?S3成立,若存在,求出λ的值;若不存在,说明理由.
分析:(1)当a=
时,如图所示,设M(
,y1),N(
,y2).则M1(-
,y1),N1(-
,y2),A(
,0).由题意可设直线MN的方程为my+
=x,与抛物线方程联立得到根与系数的关系.只要证明
•
=0即可.
(2)假设存在λ,使得对任意的a>0,均有 S22=λS1?S3成立.设M(
,y1),N(
,y2).则M1(-a,y1),N1(-a,y2),不妨设y1>0.设直线MN:my+a=x,与抛物线方程联立得到根与系数的关系,用坐标分别表示S1,S2,S3.利用 S22=λS1?S3成立即可得出λ.
| p |
| 2 |
| ||
| 2p |
| ||
| 2p |
| p |
| 2 |
| P |
| 2 |
| p |
| 2 |
| p |
| 2 |
| AM1 |
| AN1 |
(2)假设存在λ,使得对任意的a>0,均有 S22=λS1?S3成立.设M(
| ||
| 2p |
| ||
| 2p |
解答:解:(1)当a=
时,如图所示, 设M(
设M(
,y1),N(
,y2).则M1(-
,y1),N1(-
,y2),A(
,0).
则
•
=(-p,y1)•(-p,y2)=p2+y1y2.(*)
设直线MN的方程为my+
=x,联立
,化为y2-2pmx-p2=0.
∴y1y2=-p2.
代入(*)可得
•
=p2-p2=0.
∴AM1⊥AN1;
(2)假设存在λ,使得对任意的a>0,均有 S22=λS1?S3成立.
设M(
,y1),N(
,y2).则M1(-a,y1),N1(-a,y2),不妨设y1>0.
设直线MN:my+a=x,联立
,化为y2-2pmy-2pa=0.
∵△>0成立,∴y1+y2=2pm,y1y2=-2pa.
S1=
|MM1|y1=
(
+a)y1,
同理S3=
(
+a)(-y2),S2=
×2a×|y1-y2|.
∴S1S3=
(-y1y2)(
+a)(
+a)=-
y1y2[
+
(
+
)+a2]=
[
+
(4p2m2+4pa)+a2]=pa2(pm2+2a).
=a2[(y1+y2)2-4y1y2]=a2(4p2m2+8pa)=4pa2(pm2+2a),
∴4pa2(pm2+2a)=λpa2(pm2+2a),解得λ=4.
故存在λ=4,使得对任意的a>0,均有 S22=λS1?S3成立.
| p |
| 2 |
 设M(
设M(
| ||
| 2p |
| ||
| 2p |
| p |
| 2 |
| P |
| 2 |
| p |
| 2 |
则
| AM1 |
| AN1 |
设直线MN的方程为my+
| p |
| 2 |
|
∴y1y2=-p2.
代入(*)可得
| AM1 |
| AN1 |
∴AM1⊥AN1;
(2)假设存在λ,使得对任意的a>0,均有 S22=λS1?S3成立.
设M(
| ||
| 2p |
| ||
| 2p |
设直线MN:my+a=x,联立
|
∵△>0成立,∴y1+y2=2pm,y1y2=-2pa.
S1=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2p |
同理S3=
| 1 |
| 2 |
| ||
| 2p |
| 1 |
| 2 |
∴S1S3=
| 1 |
| 4 |
| ||
| 2p |
| ||
| 2p |
| 1 |
| 4 |
| ||||
| 4p2 |
| a |
| 2p |
| y | 2 1 |
| y | 2 2 |
| 2pa |
| 4 |
| 4p2a2 |
| 4p2 |
| a |
| 2p |
| S | 2 2 |
∴4pa2(pm2+2a)=λpa2(pm2+2a),解得λ=4.
故存在λ=4,使得对任意的a>0,均有 S22=λS1?S3成立.
点评:本题综合考查了抛物线的标准方程及其性质、直线与抛物线相交问题转化为方程联立得到根与系数的关系、向量垂直与数量积的关系、三角形的面积计算公式等基础知识与基本技能方法,属于难题.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
过抛物线y2=2px(p>0)的焦点F的直线l与抛物线在第一象限的交点为A,与抛物线的准线的交点为B,点A在抛物线准线上的射影为C,若
=
,
•
=48,则抛物线的方程为( )
| AF |
| FB |
| BA |
| BC |
| A、y2=4x | ||
| B、y2=8x | ||
| C、y2=16x | ||
D、y2=4
|
过抛物线y2=2px(p>0)的焦点F作直线交抛物线于A、B两点,O为抛物线的顶点.则△ABO是一个( )
| A、等边三角形 | B、直角三角形 | C、不等边锐角三角形 | D、钝角三角形 |