Question

9．△ABC中，AB=5，AC=7，△ABC的外接圆圆心为O，对于$\overrightarrow{AO}•\overrightarrow{BC}$的值，下列选项正确的是（　　）

• A． 12
• B． 10
• C． 8
• D． 不是定值

Answer 1

分析 O为△ABC外接圆圆心，可取AB边中点E，AC边中点F，连接OD，OE，AO，从而有OD⊥AB，OE⊥AC，而$\overrightarrow{AO}•\overrightarrow{BC}=\overrightarrow{AO}•\overrightarrow{AC}-\overrightarrow{AO}•\overrightarrow{AB}$，从而进行数量积的计算，便可得出该数量积的值．

解答 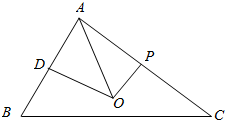解：如图，取AB中点D，AC中点E，连接OD，OE，则：
OD⊥AB，OE⊥AC；
∴$\overrightarrow{AO}•\overrightarrow{BC}=\overrightarrow{AO}•（\overrightarrow{AC}-\overrightarrow{AB}）$
=$\overrightarrow{AO}•\overrightarrow{AC}-\overrightarrow{AO}•\overrightarrow{AB}$
=$|\overrightarrow{AO}||\overrightarrow{AC}|cos∠OAE-$$|\overrightarrow{AO}||\overrightarrow{AB}|cos∠OAD$
=$AE•AC-AD•AB=\frac{49}{2}-\frac{25}{2}=12$．
故选A．

点评 考查三角形外接圆及外接圆圆心的概念，向量减法的几何意义，以及向量数量积的运算及其计算公式，直角三角形边角的关系．