题目内容
已知椭圆C的方程为 ,点A、B分别为其左、右顶点,点F1、F2分别为其左、右焦点,以点A为圆心,AF1为半径作圆A;以点B为圆心,OB为半径作圆B;若直线
,点A、B分别为其左、右顶点,点F1、F2分别为其左、右焦点,以点A为圆心,AF1为半径作圆A;以点B为圆心,OB为半径作圆B;若直线 被圆A和圆B截得的弦长之比为
被圆A和圆B截得的弦长之比为 ;
;(1)求椭圆C的离心率;
(2)己知a=7,问是否存在点P,使得过P点有无数条直线被圆A和圆B截得的弦长之比为
 ;若存在,请求出所有的P点坐标;若不存在,请说明理由.
;若存在,请求出所有的P点坐标;若不存在,请说明理由.
【答案】分析:(1)根据直线l的斜率可知直线l的倾斜角,进而可求得点A到直线l的距离,进而表示出直线l被圆A截得的弦长和被圆B截得的弦长,利用弦长之比为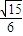 ,求得a和c的关系,进而求得e.
,求得a和c的关系,进而求得e.
(2)假设存在,设P点坐标为(m,n),过P点的直线为L,当直线L的斜率不存在时,直线L不能被两圆同时所截,故可知直线L的斜率一定存在,进而可设直线方程,求得点A(-7,0)到直线L的距离,根据(1)的离心率求得圆A的半径,同样可求得圆B的半径,则可求得直线L被两圆截得的弦长,根据他们的比为 建立等式,整理成关于k的一元二次方程,方程有无穷多解,进而求得m和n,则点P的坐标可得.
建立等式,整理成关于k的一元二次方程,方程有无穷多解,进而求得m和n,则点P的坐标可得.
解答:解:(1)由 ,得直线l的倾斜角为150°,
,得直线l的倾斜角为150°,
则点A到直线l的距离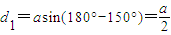 ,
,
故直线l被圆A截得的弦长为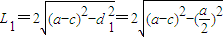 ,
,
直线l被圆B截得的弦长为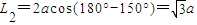 ,
,
据题意有: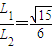 ,即
,即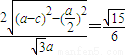
化简得:16e2-32e+7=0,
解得: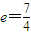 或
或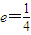 ,又椭圆的离心率e∈(0,1);
,又椭圆的离心率e∈(0,1);
故椭圆C的离心率为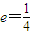 .
.
(2)假设存在,设P点坐标为(m,n),过P点的直线为L;
当直线L的斜率不存在时,直线L不能被两圆同时所截;
故可设直线L的方程为y-n=k(x-m),
则点A(-7,0)到直线L的距离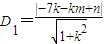 ,
,
由(1)有 ,得
,得 =
=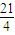 ,
,
故直线L被圆A截得的弦长为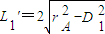 ,
,
则点B(7,0)到直线L的距离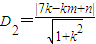 ,rB=7,
,rB=7,
故直线L被圆B截得的弦长为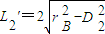 ,
,
据题意有: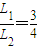 ,即有16(rA2-D12)=9(rB2-D22),整理得4D1=3D2,
,即有16(rA2-D12)=9(rB2-D22),整理得4D1=3D2,
即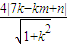 =
=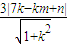 ,
,
两边平方整理成关于k的一元二次方程得(7m2+350m+343)k2-(350m+14mn)k+7n2=0,
关于k的方程有无穷多解,
故有: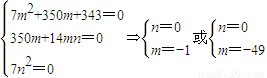 ,
,
故所求点P坐标为(-1,0)或(-49,0).
点评:本题主要考查了椭圆的性质以及直线与椭圆、圆的关系的综合考查.考查了学生综合分析问题和基本的运算能力.
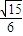 ,求得a和c的关系,进而求得e.
,求得a和c的关系,进而求得e.(2)假设存在,设P点坐标为(m,n),过P点的直线为L,当直线L的斜率不存在时,直线L不能被两圆同时所截,故可知直线L的斜率一定存在,进而可设直线方程,求得点A(-7,0)到直线L的距离,根据(1)的离心率求得圆A的半径,同样可求得圆B的半径,则可求得直线L被两圆截得的弦长,根据他们的比为
 建立等式,整理成关于k的一元二次方程,方程有无穷多解,进而求得m和n,则点P的坐标可得.
建立等式,整理成关于k的一元二次方程,方程有无穷多解,进而求得m和n,则点P的坐标可得.解答:解:(1)由
 ,得直线l的倾斜角为150°,
,得直线l的倾斜角为150°,则点A到直线l的距离
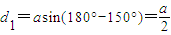 ,
,故直线l被圆A截得的弦长为
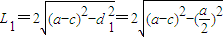 ,
,直线l被圆B截得的弦长为
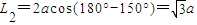 ,
,据题意有:
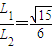 ,即
,即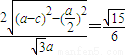
化简得:16e2-32e+7=0,
解得:
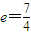 或
或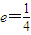 ,又椭圆的离心率e∈(0,1);
,又椭圆的离心率e∈(0,1);故椭圆C的离心率为
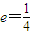 .
.(2)假设存在,设P点坐标为(m,n),过P点的直线为L;
当直线L的斜率不存在时,直线L不能被两圆同时所截;
故可设直线L的方程为y-n=k(x-m),
则点A(-7,0)到直线L的距离
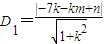 ,
,由(1)有
 ,得
,得 =
=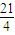 ,
,故直线L被圆A截得的弦长为
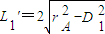 ,
,则点B(7,0)到直线L的距离
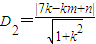 ,rB=7,
,rB=7,故直线L被圆B截得的弦长为
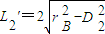 ,
,据题意有:
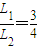 ,即有16(rA2-D12)=9(rB2-D22),整理得4D1=3D2,
,即有16(rA2-D12)=9(rB2-D22),整理得4D1=3D2,即
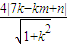 =
=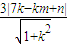 ,
,两边平方整理成关于k的一元二次方程得(7m2+350m+343)k2-(350m+14mn)k+7n2=0,
关于k的方程有无穷多解,
故有:
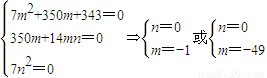 ,
,故所求点P坐标为(-1,0)或(-49,0).
点评:本题主要考查了椭圆的性质以及直线与椭圆、圆的关系的综合考查.考查了学生综合分析问题和基本的运算能力.

练习册系列答案
相关题目