题目内容
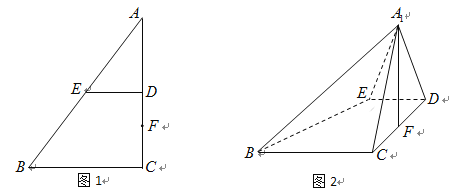
【题目】如图,一条小河岸边有相距![]() 的
的![]() 两个村庄(村庄视为岸边上
两个村庄(村庄视为岸边上![]() 两点),在小河另一侧有一集镇
两点),在小河另一侧有一集镇![]() (集镇视为点
(集镇视为点![]() ),
),![]() 到岸边的距离
到岸边的距离![]() 为
为![]() ,河宽
,河宽![]() 为
为![]() ,通过测量可知,
,通过测量可知,![]() 与
与![]() 的正切值之比为
的正切值之比为![]() .当地政府为方便村民出行,拟在小河上建一座桥
.当地政府为方便村民出行,拟在小河上建一座桥![]() (
(![]() 分别为两岸上的点,且
分别为两岸上的点,且![]() 垂直河岸,
垂直河岸,![]() 在
在![]() 的左侧),建桥要求:两村所有人到集镇所走距离之和最短,已知
的左侧),建桥要求:两村所有人到集镇所走距离之和最短,已知![]() 两村的人口数分别是
两村的人口数分别是![]() 人、
人、![]() 人,假设一年中每人去集镇的次数均为
人,假设一年中每人去集镇的次数均为![]() 次.设
次.设![]() .(小河河岸视为两条平行直线)
.(小河河岸视为两条平行直线)

(1)记![]() 为一年中两村所有人到集镇所走距离之和,试用
为一年中两村所有人到集镇所走距离之和,试用![]() 表示
表示![]() ;
;
(2)试确定![]() 的余弦值,使得
的余弦值,使得![]() 最小,从而符合建桥要求.
最小,从而符合建桥要求.
【答案】(1)![]() ,
,![]() ;(2)当
;(2)当![]() 时,符合建桥要求.
时,符合建桥要求.
【解析】
(1)利用正切值之比可求得![]() ,
,![]() ;根据
;根据![]() 可表示出
可表示出![]() 和
和![]() ,代入
,代入![]() 整理可得结果;(2)根据(1)的结论可得
整理可得结果;(2)根据(1)的结论可得![]() ,利用导数可求得
,利用导数可求得![]() 时,
时,![]() 取得最小值,得到结论.
取得最小值,得到结论.
(1)![]() 与
与![]() 的正切值之比为
的正切值之比为![]()
![]()
![]()
则![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]()
![]() ,
,![]()
![]() ,
,![]()
(2)由(1)知:![]() ,
,![]()
![]() ,
,![]()
令![]() ,解得:
,解得:![]()
令![]() ,且
,且![]()
当![]() 时,
时,![]() ,
,![]() ;当
;当![]() 时,
时,![]() ,
,![]()
![]() 函数
函数![]() 在
在![]() 上单调递减;在
上单调递减;在![]() 上单调递增;
上单调递增;
![]() 时,函数
时,函数![]() 取最小值,即当
取最小值,即当![]() 时,符合建桥要求
时,符合建桥要求

练习册系列答案
相关题目