题目内容
【题目】已知函数![]() .
.
(1)若函数![]() 与函数
与函数![]() 在
在![]() 处有相同的切线,求实数
处有相同的切线,求实数![]() 的值;
的值;
(2)当![]() 时,
时, ![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() .
.
(2)![]() .
.
【解析】
(1)根据题意,求出f(x)与g(x)的导数,由导数的几何意义可得f'(1)=g'(1),则2λ=1,解可得λ的值,即可得答案;
(2)根据题意,设h(x)=f(x)﹣g(x)=xlnx﹣λ(x2﹣1),则原问题可以转化为h(x)≤0对x∈[1,+∞)恒成立,求出h(x)的导数,利用导数与函数单调性的关系,分析可得答案.
(1)由题意得![]() ,
,
又![]() ,且函数
,且函数![]() 与
与![]() 在
在![]() 处有相同的切线,
处有相同的切线,
![]() ,则
,则![]() ,即
,即![]() .
.
(2)设![]() ,则
,则![]() 对
对![]() 恒成立.
恒成立.
![]() ,且
,且![]() ,即
,即![]() .
.
另一方面,当![]() 时,记
时,记![]() ,则
,则![]() .
.
当![]() 时,
时,![]() 在
在![]() 内为减函数,
内为减函数,
![]() 当
当![]() 时,
时,![]() ,即
,即![]() 在
在![]() 内为减函数,
内为减函数,
![]() 当
当![]() 时,
时,![]() 恒成立,符合题意.
恒成立,符合题意.
当![]() 时,
时,
①若![]() ,则
,则![]() 对
对![]() 恒成立,
恒成立,
![]() 在
在![]() 内为增函数,
内为增函数,![]() 当
当![]() 时,
时,![]() 恒成立,不符合题意.
恒成立,不符合题意.
②若![]() ,令
,令![]() ,则
,则![]()
![]() 在
在![]() 内为增函数,
内为增函数,![]() 当
当![]() 时,
时,![]() ,即
,即![]()
![]() 在
在![]() 内为增函数,
内为增函数,![]() 当
当![]() 时,
时,![]() ,不符合题意,
,不符合题意,
综上所述![]() .
.

练习册系列答案
相关题目
【题目】为了了解某省各景区在大众中的熟知度,随机从本省![]() 岁的人群中抽取了
岁的人群中抽取了![]() 人,得到各年龄段人数的频率分布直方图如图所示,现让他们回答问题“该省有哪几个国家
人,得到各年龄段人数的频率分布直方图如图所示,现让他们回答问题“该省有哪几个国家![]() 级旅游景区?”,统计结果如下表所示:
级旅游景区?”,统计结果如下表所示:
组号 | 分组 | 回答正确的人数 | 回答正确的人数占本组的频率 |
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
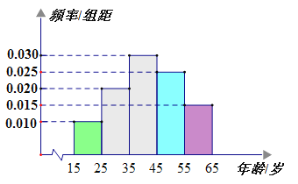
(1)分别求出![]() 的值;
的值;
(2)从第![]() 组回答正确的人中用分层抽样的方法抽取
组回答正确的人中用分层抽样的方法抽取![]() 人,求第
人,求第![]() 组每组抽取的人数;
组每组抽取的人数;
(3)在(2)中抽取的![]() 人中随机抽取
人中随机抽取![]() 人,求所抽取的人中恰好没有年龄段在
人,求所抽取的人中恰好没有年龄段在![]() 的概率
的概率

