题目内容
若α∈(0,| π |
| 2 |
| π |
| 2 |
| 3 |
| 5 |
(1)sin(α-
| π |
| 3 |
(2)tanβ
分析:(1)利用同角三角函数的关系,先求sinα=
,再利用差角的正弦公式可求;(2)由(1)知tanα=
,再由β=α-(α-β),利用差角的正切公式可求.
| 4 |
| 5 |
| 4 |
| 3 |
,再由β=α-(α-β),利用差角的正切公式可求.
解答:解:(1)α∈(0,
)且cosα=
,∴sinα=
∴sin(α-
)=sinαcos
-cosαsin
=
×
-
×
=
(2)由(1)知tanα=
∴tanβ=tan[α-(α-β)]=
=
=-
| π |
| 2 |
| 3 |
| 5 |
| 4 |
| 5 |
∴sin(α-
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| 4 |
| 5 |
| 1 |
| 2 |
| 3 |
| 5 |
| ||
| 2 |
4-3
| ||
| 10 |
(2)由(1)知tanα=
| 4 |
| 3 |
∴tanβ=tan[α-(α-β)]=
| tanα-tan(α-β) |
| 1+tanα•tan(α-β) |
| ||
1-
|
| 13 |
| 9 |
点评:本题主要考查三角恒等变换,正确的拆、配角是解题的关键.

练习册系列答案
相关题目
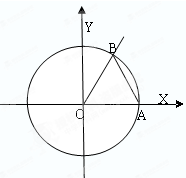 如图,在平面直角坐标系xoy中,角α的始边与x轴的非负半轴重合且与单位圆相交于A点,它的终边与单位圆相交于x轴上方一点B,始边不动,终边在运动.
如图,在平面直角坐标系xoy中,角α的始边与x轴的非负半轴重合且与单位圆相交于A点,它的终边与单位圆相交于x轴上方一点B,始边不动,终边在运动.