题目内容
【题目】如图所示,在四棱锥P﹣ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE.
(1)证明:BD⊥平面PAC;
(2)若PA=1,AD=2,求二面角B﹣PC﹣A的正切值.
【答案】
(1)解:∵PA⊥平面ABCD
∴PA⊥BD
∵PC⊥平面BDE
∴PC⊥BD,又PA∩PC=P
∴BD⊥平面PAC
(2)解:设AC与BD交点为O,连OE
∵PC⊥平面BDE
∴PC⊥平面BOE
∴PC⊥BE
∴∠BEO为二面角B﹣PC﹣A的平面角
∵BD⊥平面PAC
∴BD⊥AC
∴四边形ABCD为正方形,又PA=1,AD=2,可得BD=AC=2 ![]() ,PC=3
,PC=3
∴OC= ![]()
在△PAC∽△OEC中, ![]()
又BD⊥OE,
∴ ![]()
∴二面角B﹣PC﹣A的平面角的正切值为3
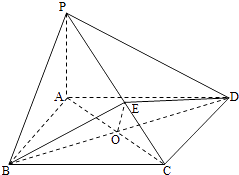
【解析】(1)由题设条件及图知,可先由线面垂直的性质证出PA⊥BD与PC⊥BD,再由线面垂直的判定定理证明线面垂直即可;(2)由图可令AC与BD的交点为O,连接OE,证明出∠BEO为二面角B﹣PC﹣A的平面角,然后在其所在的三角形中解三角形即可求出二面角的正切值.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目