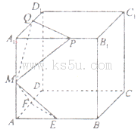
题目内容
【题目】一个盒子中装有2个红球，4个白球，除颜色外，它们的形状、大小、质量等完全相同
（1）采用不放回抽样，先后取两次，每次随机取一个球，求恰好取到1个红球，七个白球的概率；
（2）采用放回抽样，每次随机抽取一球，连续取3次，求至少有1次取到红球的概率.
【答案】（1）
（2）
【解析】试题分析：（1）不放回的先后取两次，第一次有6种不同的取法，第二次有5种不同的取法，所以一共有6×5=30种不同的取法种数，若恰第一次取红球，第二次取白球共有2×4=8种，若第一次取白球，第二次取红球，共有4×2=8种，所以恰好取到一个红球的种数为16种，所以概率为
；（2）若放回抽取，每次取一球，连续3次，则不同的取法种数为6×6×6=216种，若3次都取到白球，共有 4×4×4=64种，所以根据对立事件概率加法公式可知，至少有1次取得红球的概率为
.
试题解析：（1）恰好取到1个红球，1个白球的概率为
（2）采用放回抽样，每次取到红球的概率
，∴至少有1次取到红球的概率为
.
练习册系列答案
相关题目
