题目内容
函数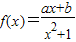 是奇函数,且
是奇函数,且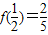 ,
,(1)求f(x)的解析式;
(2)证明:f(x)在(-1,1)上是增函数.
【答案】分析:先根据函数为奇函数即f(-x)=-f(x)求得b=0,再根据 求得a=1,得到f(x)的解析式;利用增函数的定义证明f(x)的单调性.
求得a=1,得到f(x)的解析式;利用增函数的定义证明f(x)的单调性.
解答:解:(1)f(0)=0得,b=0,再根据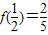 ,得a=1,∴
,得a=1,∴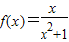
(2) ,令f′(x)>0得x∈(-1,1),
,令f′(x)>0得x∈(-1,1),
∴f(x)在(-1,1)上是增函数.
点评:本题考查了函数奇偶性及函数的单调性,函数的性质是高考考试的热点,要会运用函数的奇偶性和单调性进行解题.证明函数的单调性的方法为:定义法和导数法.属基础题.
 求得a=1,得到f(x)的解析式;利用增函数的定义证明f(x)的单调性.
求得a=1,得到f(x)的解析式;利用增函数的定义证明f(x)的单调性.解答:解:(1)f(0)=0得,b=0,再根据
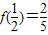 ,得a=1,∴
,得a=1,∴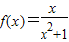
(2)
 ,令f′(x)>0得x∈(-1,1),
,令f′(x)>0得x∈(-1,1),∴f(x)在(-1,1)上是增函数.
点评:本题考查了函数奇偶性及函数的单调性,函数的性质是高考考试的热点,要会运用函数的奇偶性和单调性进行解题.证明函数的单调性的方法为:定义法和导数法.属基础题.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
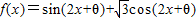 是奇函数,且在
是奇函数,且在 上是减函数的θ的一个值是( )
上是减函数的θ的一个值是( )

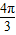
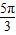
 是奇函数,且满足
是奇函数,且满足
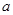 、
、 的值;
的值;
 在区间
在区间 单调递减,在区间
单调递减,在区间 单调递增;
单调递增; 同时满足以下两个条件:①不等式
同时满足以下两个条件:①不等式 对
对 恒成立;
恒成立;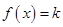 在
在 上有解.若存在,试求出实数
上有解.若存在,试求出实数 是奇函数,且在
是奇函数,且在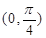 上是增函数,则实数
上是增函数,则实数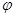 可能是(▲)
可能是(▲)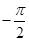 B.
B. C.
C. D.
D.