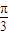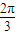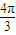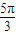题目内容
使函数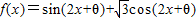 是奇函数,且在
是奇函数,且在 上是减函数的θ的一个值是( )
上是减函数的θ的一个值是( )A.

B.

C.
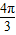
D.
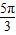
【答案】分析:利用两角和正弦公式化简函数的解析式为 2sin(2x+θ+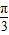 ),由于它是奇函数,故θ+
),由于它是奇函数,故θ+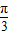 =kπ,k∈z,当k为奇数时,
=kπ,k∈z,当k为奇数时,
f(x)=-2sin2x,满足在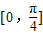 上是减函数,此时,θ=2nπ-
上是减函数,此时,θ=2nπ-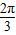 ,n∈z,当k为偶数时,经检验不满足条件.
,n∈z,当k为偶数时,经检验不满足条件.
解答:解:∵函数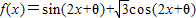 =2sin(2x+θ+
=2sin(2x+θ+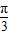 ) 是奇函数,故θ+
) 是奇函数,故θ+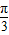 =kπ,k∈z,θ=kπ-
=kπ,k∈z,θ=kπ-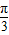 .
.
当k为奇数时,令k=2n-1,f(x)=-2sin2x,满足在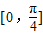 上是减函数,此时,θ=2nπ-
上是减函数,此时,θ=2nπ-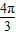 ,n∈z,
,n∈z,
选项B满足条件.
当k为偶数时,令k=2n,f(x)=2sin2x,不满足在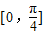 上是减函数.
上是减函数.
综上,只有选项B满足条件.
故选 B.
点评:本题考查两角和正弦公式,正弦函数的单调性,奇偶性,体现了分类讨论的数学思想,化简函数的解析式是解题的突破口.
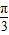 ),由于它是奇函数,故θ+
),由于它是奇函数,故θ+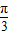 =kπ,k∈z,当k为奇数时,
=kπ,k∈z,当k为奇数时,f(x)=-2sin2x,满足在
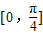 上是减函数,此时,θ=2nπ-
上是减函数,此时,θ=2nπ-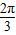 ,n∈z,当k为偶数时,经检验不满足条件.
,n∈z,当k为偶数时,经检验不满足条件.解答:解:∵函数
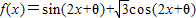 =2sin(2x+θ+
=2sin(2x+θ+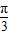 ) 是奇函数,故θ+
) 是奇函数,故θ+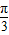 =kπ,k∈z,θ=kπ-
=kπ,k∈z,θ=kπ-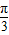 .
.当k为奇数时,令k=2n-1,f(x)=-2sin2x,满足在
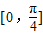 上是减函数,此时,θ=2nπ-
上是减函数,此时,θ=2nπ-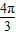 ,n∈z,
,n∈z,选项B满足条件.
当k为偶数时,令k=2n,f(x)=2sin2x,不满足在
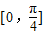 上是减函数.
上是减函数.综上,只有选项B满足条件.
故选 B.
点评:本题考查两角和正弦公式,正弦函数的单调性,奇偶性,体现了分类讨论的数学思想,化简函数的解析式是解题的突破口.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
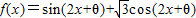 是奇函数,且在
是奇函数,且在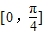 上是减函数的θ的一个值是( )
上是减函数的θ的一个值是( )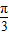
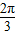
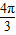
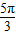
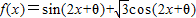 是奇函数,且在
是奇函数,且在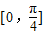 上是减函数的θ的一个值是( )
上是减函数的θ的一个值是( )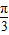
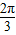
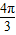
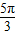
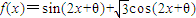 是奇函数,且在
是奇函数,且在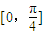 上是减函数的θ的一个值是( )
上是减函数的θ的一个值是( )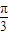
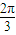
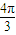
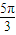
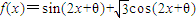 是奇函数,且在
是奇函数,且在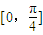 上是减函数的θ的一个值是( )
上是减函数的θ的一个值是( )