题目内容
已知存在实数![]() (其中
(其中![]() )使得函数
)使得函数![]() 是奇函数,且在
是奇函数,且在![]() 上是增函数。
上是增函数。
(1)试用观察法猜出两组![]() 与
与![]() 的值,并验证其符合题意;
的值,并验证其符合题意;
(2)求出所有符合题意的![]() 与
与![]() 的值。
的值。
(1)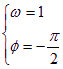 或
或 ;所有符合题意的
;所有符合题意的![]() 与
与![]() 的值为:
的值为:
(2)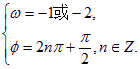 或
或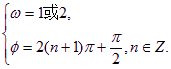
解析:
(1)猜想: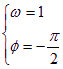 或
或 ;---------------------4分
;---------------------4分
由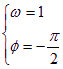 知
知![]() ,而
,而![]() 为奇函数且在
为奇函数且在![]() 上是增函数。--------------------------------------6分
上是增函数。--------------------------------------6分
由 知
知![]() ,而
,而![]() 为奇函数且在
为奇函数且在![]() 上是增函数。----------------------------8分
上是增函数。----------------------------8分
(2)由![]() 为奇函数,有
为奇函数,有![]()
所以![]() ,又
,又![]() ,
,
解得![]() 。--------------------------------------------------10分
。--------------------------------------------------10分
当![]() 时,
时,![]() 为奇函数,由于
为奇函数,由于![]() 在
在![]() 上是增函数,所以
上是增函数,所以![]() ,由
,由![]() ,又
,又![]() 在
在![]() 上是增函数,故有
上是增函数,故有![]() ,且
,且![]() 或
或![]() ,故
,故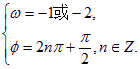 。-------------------------12分
。-------------------------12分
当![]() 时,
时,![]() 为奇函数,由于
为奇函数,由于![]() 在
在![]() 上是增函数,所以
上是增函数,所以![]() ,由
,由![]() ,又
,又![]() 在
在![]() 上是增函数,故有
上是增函数,故有![]() ,且
,且![]() 或2,故
或2,故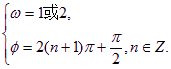 --------------------------------------14分
--------------------------------------14分
所以所有符合题意的![]() 与
与![]() 的值为:
的值为:
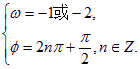 或
或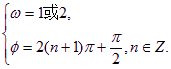 -------------------------16分
-------------------------16分

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案
相关题目
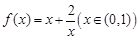 的最小值是
的最小值是 ;②对于任意实数
;②对于任意实数 ,有
,有 且
且 时,
时, ,
,
 ,则
,则 时,
时, ;③如果
;③如果 是可导函数,则
是可导函数,则 是函数
是函数 处取到极值的必要不充分条件;④已知存在实数
处取到极值的必要不充分条件;④已知存在实数 成立,则实数
成立,则实数 的取值范围是
的取值范围是 。其中正确的命题是___________.
。其中正确的命题是___________.