题目内容
设函数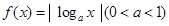 的定义域为
的定义域为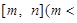
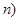 ,值域为
,值域为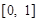 ,若
,若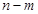 的最小值为
的最小值为 ,则实数a的值为(
)
,则实数a的值为(
)
A.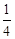 B.
B.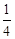 或
或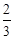 C.
C.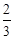 D.
D.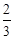 或
或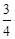
【答案】
D
【解析】
试题分析:①若1≤m<n,则f(x)=-logax,
∵f(x)的值域为[0,1],∴f(m)=0,f(n)=1,解得m=1,n=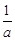 ,
,
又∵n-m的最小值为 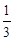 ,∴
,∴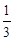 -1≥
-1≥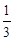 ,及0<a<1,当等号成立时,解得a=
,及0<a<1,当等号成立时,解得a=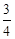 .
.
②若0<m<n<1,则f(x)=logax,
∵f(x)的值域为[0,1],∴f(m)=1,f(n)=0,解得m=a,n=1,又∵n-m的最小值为 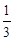 ,∴1-a≥
,∴1-a≥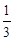 ,
,
及0<a<1,当等号成立时,解得a=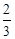 .
.
③若0<m<1<n时,不满足题意,故选D。
考点:本题主要考查对数函数的性质,绝对值的概念。
点评:中档题,注意运用分类讨论思想,确定m,n,的可能情况。本题易错,忽视不同情况的讨论。

练习册系列答案
相关题目
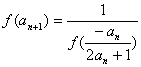 (n∈N*)
(n∈N*) .
. 的定义域为集合B,若A⊆B,求实数a的取值范围.
的定义域为集合B,若A⊆B,求实数a的取值范围.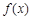 的定义域为
的定义域为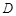 ,若存在非零实数
,若存在非零实数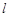 使得对于任意
使得对于任意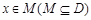 ,有
,有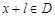 ,且
,且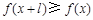 ,则称
,则称 上的
上的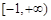 的函数
的函数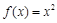 为
为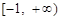 上的
上的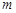 高调函数,那么实数
高调函数,那么实数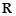 的函数
的函数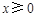 时,
时,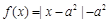 ,且
,且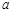 的取值范围是 .
的取值范围是 .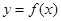 的定义域为R,当
的定义域为R,当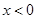 时,
时, ,且对任意实数
,且对任意实数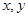 ,都有
,都有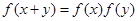 成立,数列
成立,数列 满足
满足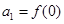 且
且
 的值;
的值;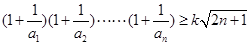 对一切
对一切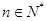 均成立,求
均成立,求 的最大值.
的最大值.