Question

（09年东城区示范校质检一）（本小题满分14分）

设函数的定义域为全体R，当x<0时，，且对任意的实数x，y∈R，有成立，数列满足，且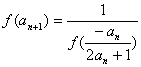（n∈N^*）

   （Ⅰ）求证：是R上的减函数；

   （Ⅱ）求数列的通项公式；

   （Ⅲ）若不等式对一切n∈N^*均成立，求k的

最大值．

Answer 1

解析：（Ⅰ）令，得，

由题意知，所以，故．

    当时，，，进而得．

       设且，则，

．

即，所以是R上的减函数．       ………………-4分

（Ⅱ）由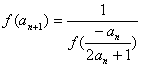 得  ，

所以．

因为是R上的减函数，所以，  ………………6分

即， 进而，

所以是以1为首项，2为公差的等差数列．

所以，           

所以．                                      ………………9分

（Ⅲ）由对一切n∈N^*均成立．

知对一切n∈N^*均成立．

    设，

知且

   又．

故为关于n的单调增函数，．

所以，k的最大值为                     ………………14分