题目内容
【题目】已知函数![]() ,
, ![]() ,其中
,其中![]() 为自然对数的底数.
为自然对数的底数.
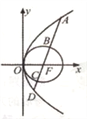
(1)若![]() ,求曲线
,求曲线![]() 在点
在点![]() 处的切线斜率;
处的切线斜率;
(2)证明:当![]() 时,函数
时,函数![]() 有极小值,且极小值大于
有极小值,且极小值大于![]() .
.
【答案】(1) ![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】试题分析:(1)由![]() ,可得
,可得![]() ,故
,故![]() ,即曲线
,即曲线![]() 在点
在点![]() 处的切线斜率
处的切线斜率![]() ;(2)由
;(2)由![]() 在区间
在区间![]() 上是单调递增函数,可得存在
上是单调递增函数,可得存在![]() 使得
使得![]() ,使得
,使得![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增, ![]() 在区间
在区间![]() 上有极小值
上有极小值![]() ,设
,设![]() ,
, ![]() ,利用导数研究函数的单调性,可得
,利用导数研究函数的单调性,可得![]() 在
在![]() 上单调递减,所以
上单调递减,所以![]() .
.
试题解析:(1)依题意, ![]() ,
, ![]() ,故
,故![]() ,
,
即曲线![]() 在点
在点![]() 处的切线斜率为
处的切线斜率为![]() ;
;
证明:(2)因为![]() ,所以
,所以![]() 在区间
在区间![]() 上是单调递增函数,
上是单调递增函数,
因为![]() ,
, ![]() ,
,
所以![]() 使得
使得![]() ,
,
所以![]() ,
, ![]() ;
; ![]() ,
, ![]() ,
,
故![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
所以![]() 在区间
在区间![]() 上有极小值
上有极小值![]() ,
,
因为![]() ,所以
,所以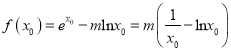 ,
,
设![]() ,
, ![]() ,
,
则![]()
![]() ,所以
,所以![]() ,
,
即![]() 在
在![]() 上单调递减,所以
上单调递减,所以![]() ,
,
即![]() ,故当
,故当![]() 时,函数
时,函数![]() 有极小值,且极小值大于
有极小值,且极小值大于![]() .
.

 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案【题目】某城市随机抽取一年(365天)内100天的空气质量指数![]() (Air Pollution Index)的监测数据,结果统计如下:
(Air Pollution Index)的监测数据,结果统计如下:
|
|
|
|
|
|
| 大于300 |
空气质量 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中度重 污染 | 重度污染 |
天数 | 10 | 15 | 20 | 30 | 7 | 6 | 12 |
(Ⅰ)若本次抽取的样本数据有30天是在供暖季,其中有7天为重度污染,完成下面![]() 列联表,并判断能否有
列联表,并判断能否有![]() 的把握认为该市本年空气重度污染与供暖有关?
的把握认为该市本年空气重度污染与供暖有关?
非重度污染 | 重度污染 | 合计 | |
供暖季 | |||
非供暖季 | |||
合计 | 100 |
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 1.323 | 2.072 | 2.706 | 3.841 5.024 | 6.635 | 7.879 | 10.828 |
附: 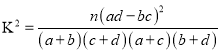
(Ⅱ)政府要治理污染,决定对某些企业生产进行管控,当![]() 在区间
在区间![]() 时企业正常生产;当
时企业正常生产;当![]() 在区间
在区间![]() 时对企业限产
时对企业限产![]() (即关闭
(即关闭![]() 的产能),当
的产能),当![]() 在区间
在区间![]() 时对企业限产
时对企业限产![]() ,当
,当![]() 在300以上时对企业限产
在300以上时对企业限产![]() ,企业甲是被管控的企业之一,若企业甲正常生产一天可得利润2万元,若以频率当概率,不考虑其他因素:
,企业甲是被管控的企业之一,若企业甲正常生产一天可得利润2万元,若以频率当概率,不考虑其他因素:
①在这一年中随意抽取5天,求5天中企业被限产达到或超过![]() 的恰为2天的概率;
的恰为2天的概率;
②求企业甲这一年因限产减少的利润的期望值.