题目内容
(本题满分16分)已知圆C:x2+y2+x-6y+m=0.
(1)若圆M:![]() 与圆C相交于A、B两点,且两圆在点A处的切线互相垂直,求m的值.
与圆C相交于A、B两点,且两圆在点A处的切线互相垂直,求m的值.
(2)若直线x+2y-3=0与圆C相交于P,Q两点,O为原点,且OP^OQ,求该圆的半径.
解:(1)由题知:M(0,0),C(![]() ,3),MA^CA,
,3),MA^CA,
所以![]() ,所以m=1 …………………………5分
,所以m=1 …………………………5分
(2)法一:设P(x1,y1),Q(x2,y2),由OP^OQ, 得::kOPkOQ= -1,即= -1
即x1x2+y1y2=0 ① …………………………7分
另一方面(x1,y1),(x2,y2)是方程组的实数解,
即x1,x2是5x2+10x+4m-27=0 ② 的两个实数根,
∴x1+x2=-2,x1x2= ③ …………………………10分
又P、Q在直线x+2y-3=0上,∴y1y2=(3-x1)(3-x2)= [9-3(x1+x2)+x1x2]
将③代入得y1y2= ④ ……………12分
将③④代入①知:m=3. …………………………14分
代入方程②检验D>0成立. …………………………15分
∴半径为![]() …………………………16分
…………………………16分
法二:将3=x+2y代入圆的方程知:x2+y2+(x+2y)(x-6y)+ (x+2y)2=0,……………7分
整理得:(12+m)x2+4(m-3)x y+(4m-27)y2=0
由于x≠0,可得(4m-27)( )2+4(m-3) +12+m=0, …………………………10分
∴kOP, kOQ是上方程的两根, 由kOPkOQ= -1知: =-1, ……………………14分
解得:m=3. 检验知满足题意 …………………………15分
∴半径为![]() …………………………16分
…………………………16分

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 ,且对任意
,且对任意 ,有
,有 .
. ;
; 在区间(0,1)上为单调函数,求实
在区间(0,1)上为单调函数,求实 数
数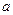 的取值范围.
的取值范围. 的零点个数?(提示
的零点个数?(提示 )
) 为实常数).
为实常数). 时,求函数
时,求函数 在
在 上的最小值;
上的最小值; 在区间
在区间 上有解,求实数
上有解,求实数 的取值范围;
的取值范围;
 )
) :
: 的离心率为
的离心率为 ,
, 分别为椭圆
分别为椭圆 为椭圆上任意一点,以
为椭圆上任意一点,以 为半径作圆
为半径作圆 有公共点时,求△
有公共点时,求△ 面积的最大值.
面积的最大值. 是定义在
是定义在 上的偶函数,且当
上的偶函数,且当 时,
时, 。
。 及
及 的值;
的值; 上的解析式;
上的解析式; 的方程
的方程 有四个不同的实数解,求实数
有四个不同的实数解,求实数 的取值范围。
的取值范围。