题目内容
【题目】如图,在几何体![]() 中,底面四边形
中,底面四边形![]() 是边长为4的菱形,
是边长为4的菱形,![]() ,
,![]() ,
,![]() ,
,![]() 平面
平面![]() ,且
,且![]() ,
,![]() .
.

(1)证明:平面![]() 平面
平面![]() ;
;
(2)求三棱锥![]() 的体积.
的体积.
【答案】(1)见解析.(2) ![]() .
.
【解析】
(1)由题意结合线面垂直的性质定理和勾股定理可证得![]() 平面
平面![]() ,然后结合面面垂直的判定定理即可证得题中的结论;
,然后结合面面垂直的判定定理即可证得题中的结论;
(2)利用线面平行进行等价转化可知![]() ,将原问题转化为求解四棱锥
,将原问题转化为求解四棱锥![]() 体积的问题,然后求得三棱锥的高即可确定其体积.
体积的问题,然后求得三棱锥的高即可确定其体积.
(1)因为![]() 平面
平面![]() ,所以
,所以![]() ,
,
又![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() ,
,
所以![]() .
.
因为四边形![]() 是边长为4的菱形,
是边长为4的菱形,![]() ,
,
所以![]() 与
与![]() 均为等边三角形,
均为等边三角形,![]() .
.
所以![]() ,
,![]() ,
,![]() ,
,
则![]() ,
,
所以![]() ,
,
又![]() ,
,![]() ,
,
所以![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() .
.
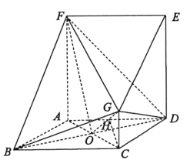
(2)因为![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
所以![]() ,
,
取![]() 的中点
的中点![]() ,连接
,连接![]() ,则
,则![]() ,
,![]() ,
,
由![]() 平面
平面![]() ,所以
,所以![]() ,又
,又![]() ,
,
所以![]() 平面
平面![]() .
.
所以![]()
![]() .
.
即三棱锥![]() 的体积为
的体积为![]() .
.

【题目】随着人们经济收入的不断增加,个人购买家庭轿车已不再是一种时尚,车的使用费用,尤其是随着使用年限的增多,所支出的费用到底会增长多少,一直是购车一族非常关心的问题,某汽车销售公司做了一次抽样调查,并统计得出2009年出售的某款车的使用年限![]() (2009年记
(2009年记![]() )与所支出的总费用
)与所支出的总费用![]() (万元)有如表的数据资料:
(万元)有如表的数据资料:
使用年限 | 2 | 3 | 4 | 5 | 6 |
总费用 | 2.5 | 3.5 | 5.5 | 6.5 | 7.0 |
(1)求线性回归方程![]() ;
;
(2)若这款车一直使用到2020年,估计使用该款车的总费用是多少元?
线性回归方程![]() 中斜率和截距用最小二乘法估计计算公式如下:
中斜率和截距用最小二乘法估计计算公式如下:
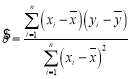
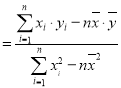 ,
,![]()
【题目】一项针对都市熟男(三线以上城市,![]() 岁男性)消费水平的调查显示,对于最近一年内是否购买过以下七类高价商品,全体被调查者,以及其中包括的1980年及以后出生(80后)被调查者,1980年以前出生(80前)被调查者回答“是”的比例分别如下:
岁男性)消费水平的调查显示,对于最近一年内是否购买过以下七类高价商品,全体被调查者,以及其中包括的1980年及以后出生(80后)被调查者,1980年以前出生(80前)被调查者回答“是”的比例分别如下:
全体被调查者 | 80后被调查者 | 80前被调查者 | |
电子产品 | 56.9% | 66.0% | 48.5% |
服装 | 23.0% | 24.9% | 21.2% |
手表 | 14.3% | 19.4% | 9.7% |
运动、户外用品 | 10.4% | 11.1% | 9.7% |
珠宝首饰 | 8.6% | 10.8% | 6.5% |
箱包 | 8.1% | 11.3% | 5.1% |
个护与化妆品 | 6.6% | 6.0% | 7.2% |
以上皆无 | 25.3% | 17.9% | 32.1% |
根据表格中数据判断,以下分析错误的是( )
A. 都市熟男购买比例最高的高价商品是电子产品
B. 从整体上看,80后购买高价商品的意愿高于80前
C. 80前超过3成一年内从未购买过表格中七类高价商品
D. 被调查的都市熟男中80后人数与80前人数的比例大约为![]()