题目内容
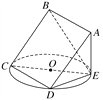
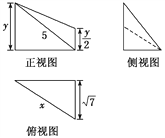
【题目】某几何体的三视图如图所示，当xy取得最大值时，该几何体的体积是________．
【答案】3
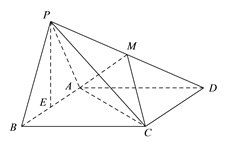
【解析】由题意可知，该几何体为如图所示的四棱锥PABCD，CD＝
，AB＝y，AC＝5，CP＝
，BP＝x，
∴BP2＝BC2＋CP2，
即x2＝25－y2＋7，x2＋y2＝32≥2xy，
则xy≤16，当且仅当x＝y＝4时，等号成立．
此时该几何体的体积V＝
＝3
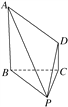
点睛:空间几何体体积问题的常见类型及解题策略
(1)若所给定的几何体是可直接用公式求解的柱体、锥体或台体，则可直接利用公式进行求解．
(2)若所给定的几何体的体积不能直接利用公式得出，则常用转换法、分割法、补形法等方法进行求解．
(3)若以三视图的形式给出几何体，则应先根据三视图得到几何体的直观图，然后根据条件求解．
练习册系列答案
相关题目
【题目】在某批次的某种灯泡中，随机地抽取
个样品，并对其寿命进行追踪调查，将结果列成频率分布表如下．根据寿命将灯泡分成优等品、正品和次品三个等级，其中寿命大于或等于
天的灯泡是优等品，寿命小于
天的灯泡是次品，其余的灯泡是正品．
寿命（天） | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
|
（Ⅰ）根据频率分布表中的数据，写出
， 
的值．
（Ⅱ）某人从灯泡样品中随机地购买了
个，求
个灯泡中恰有一个是优等品的概率．
（Ⅲ）某人从这个批次的灯泡中随机地购买了
个进行使用，若以上述频率作为概率，用
表示此人所购买的灯泡中次品的个数，求
的分布列和数学期望．
