题目内容
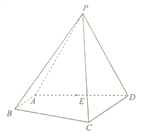
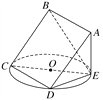
【题目】(2017·安徽名校阶段性测试)如图所示，正方形ABCD所在平面与圆O所在平面相交于CD，线段CD为圆O的弦，AE垂直于圆O所在平面，垂足E是圆O上异于C，D的点，AE＝3，圆O的直径CE＝9.
(1)求证：平面ABE⊥平面ADE；
(2)求五面体ABCDE的体积．
【答案】（1）见解析（2）
【解析】试题分析:(1) 先由线面垂直性质定理得AE⊥CD. 再由圆的性质得CD⊥DE，由线面垂直判定定理得CD⊥平面ADE. 最后根据平行得AB⊥平面ADE.,由面面垂直判定定理得结论( 2)先将五面体分割成两个三棱锥B-ADE和B-CDE,两个三棱锥的高为AB,AE,最后代入锥体体积公式即得结果
试题解析:解：(1)证明：∵AE垂直于圆O所在平面，CD圆O所在平面，∴AE⊥CD.
又CD⊥DE，AE∩DE＝E，AE平面ADE，DE平面ADE，
∴CD⊥平面ADE.
在正方形ABCD中，CD∥AB，
∴AB⊥平面ADE.
又AB平面ABE，
∴平面ABE⊥平面ADE.
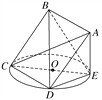
(2)连接AC，BD，设正方形ABCD的边长为a，则AC＝
a，
又AC2＝CE2＋AE2＝90，
∴a＝3
，DE＝6，
∴VBADE＝
BA·S△ADE
＝×3×
＝9.
又AB∥CD，CD平面CDE，
∴点B到平面CDE的距离等于点A到平面CDE的距离，即AE，
∴VBCDE＝AE·S△CDE＝×3×
＝9，
故VABCDE＝VBCDE＋VBADE＝18.
练习册系列答案
相关题目
