题目内容
15.已知数列{an}是一个等差数列,且a2=1,a5=$\frac{1}{5}$(1)求数列{an}的通项公式;
(2)求数列{an}的前n项和为Sn的最大值.
分析 (1)利用等差数列的通项公式即可得出;
(2)由an≥0,解得$n≤\frac{23}{4}$,可得数列{an}的前n项和的最大值为S4.
解答 解:(1)设等差数列{an}的公差为d,
∵a2=1,a5=$\frac{1}{5}$,
∴$\frac{1}{5}$=1+3d,解得d=-$\frac{4}{15}$.
∴an=1-$\frac{4}{15}(n-2)$=$\frac{23-4n}{15}$;
(2)由an≥0,解得$n≤\frac{23}{4}$,
∴数列{an}的前n项和的最大值为S4=$4×(1+\frac{4}{15})$+$\frac{4×3}{2}×(-\frac{4}{15})$=$\frac{52}{15}$.
点评 本题考查了等差数列的通项公式与前n项和公式及其性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.若a<b<c,则下列结论中正确的是( )
| A. | a|c|<b|c| | B. | ab<bc | C. | a-c<b-c | D. | $\frac{1}{a}>\frac{1}{b}>\frac{1}{c}$ |
14.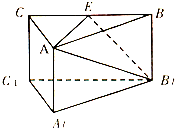 如图,三棱柱中,侧棱AA1⊥底面A1B1C1,三角形A1B1C1是正三角形,E是BC中点,则下列叙述正确的是( )
如图,三棱柱中,侧棱AA1⊥底面A1B1C1,三角形A1B1C1是正三角形,E是BC中点,则下列叙述正确的是( )
 如图,三棱柱中,侧棱AA1⊥底面A1B1C1,三角形A1B1C1是正三角形,E是BC中点,则下列叙述正确的是( )
如图,三棱柱中,侧棱AA1⊥底面A1B1C1,三角形A1B1C1是正三角形,E是BC中点,则下列叙述正确的是( )| A. | CC1与B1E是异面直线 | B. | A1C1⊥平面ABB1A1 | ||
| C. | AE,B1C1为异面直线,且AE⊥B1C1 | D. | A1C1∥平面A1EB |
 如图,四棱锥P-ABCD中,PD⊥平面ABCD,△ABD是边长为3的正三角形,BC=CD=$\sqrt{3}$,PD=4.
如图,四棱锥P-ABCD中,PD⊥平面ABCD,△ABD是边长为3的正三角形,BC=CD=$\sqrt{3}$,PD=4. 如图,AB是圆O的直径,直线CE和圆O相切于点C,AD⊥CE于D,若AD=1,∠ABC=30°,则圆O的面积是4π.
如图,AB是圆O的直径,直线CE和圆O相切于点C,AD⊥CE于D,若AD=1,∠ABC=30°,则圆O的面积是4π. 如图,AB是圆O的直径,点C在圆O上,延长BC到D使BC=CD,过C作圆O的切线交AD于E.若AB=8,DC=4,则DE=2.
如图,AB是圆O的直径,点C在圆O上,延长BC到D使BC=CD,过C作圆O的切线交AD于E.若AB=8,DC=4,则DE=2.