题目内容
已知椭圆![]() 的中心为原点,点
的中心为原点,点![]()
![]() 是它的一个焦点,直线
是它的一个焦点,直线![]() 过点
过点![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且当直线
两点,且当直线![]() 垂直于
垂直于![]() 轴时,
轴时,![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)是否存在直线![]() ,使得在直线
,使得在直线![]() 上可以找到一点
上可以找到一点![]() ,满足
,满足![]() 为正三角形.如果存在,求出直线
为正三角形.如果存在,求出直线![]() 的方程;如果不存在,请说明理由.
的方程;如果不存在,请说明理由.
解:(Ⅰ)设椭圆![]() 的方程为:
的方程为:![]() ,则
,则![]() …①
…①
![]() 当
当![]() 垂直于
垂直于![]() 轴时,
轴时,![]() 两点坐标分别是
两点坐标分别是![]() 和
和![]() ,
,
![]() ,则
,则![]() ,即
,即![]() .………②
.………②
由①,②消去![]() ,得
,得![]() .
.
![]() 或
或![]() (舍去).
(舍去).
当![]() 时,
时,![]() .
.
因此,椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)设存在满足条件的直线![]() .
.
(1) 当直线![]() 垂直于
垂直于![]() 轴时,由(Ⅰ)的解答可知
轴时,由(Ⅰ)的解答可知![]() ,焦点
,焦点![]() 到直线
到直线![]()
的距离为![]() ,此时不满足
,此时不满足![]() .
.
因此,当直线![]() 垂直于
垂直于![]() 轴时不满足条件.
轴时不满足条件.
(2)当直线![]() 不垂直于
不垂直于![]() 轴时,设直线
轴时,设直线![]() 的斜率为
的斜率为![]() ,则直线
,则直线![]() 的方程为
的方程为![]() .
.
由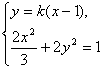
![]()
![]() ,
,
设![]() 两点的坐标分别为
两点的坐标分别为![]() 和
和![]() ,则
,则
![]() ,
,![]() .
.
![]()
![]()
![]() .
.
又设![]() 的中点为
的中点为![]() ,则
,则![]()
![]() .
.
当![]() 为正三角形时,直线
为正三角形时,直线![]() 的斜率为
的斜率为![]() .
.
![]() ,
,
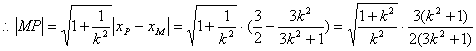 .
.
当![]() 为正三角形时,
为正三角形时,![]() ,即
,即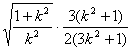 =
=![]() ,
,
解得![]() ,
,![]() .
.
因此,满足条件的直线![]() 存在,且直线
存在,且直线![]() 的方程为
的方程为![]() 或
或![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 已知椭圆的中心为原点O,一个焦点为F
已知椭圆的中心为原点O,一个焦点为F ,长轴在
,长轴在 轴上,上顶点为
轴上,上顶点为 ,左、右焦点分别为
,左、右焦点分别为 ,线段
,线段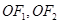 的中点分别为
的中点分别为 ,且△
,且△ 是面积为4的直角三角形。(Ⅰ)求该椭圆的离心率和标准方程;
是面积为4的直角三角形。(Ⅰ)求该椭圆的离心率和标准方程; 作直线
作直线 交椭圆于
交椭圆于 ,
, ,求直线
,求直线
 ,长轴在
,长轴在 轴上,上顶点为
轴上,上顶点为 ,左、右焦点分别为
,左、右焦点分别为 ,线段
,线段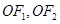 的中点分别为
的中点分别为 ,且△
,且△ 是面积为4的直角三角形。(Ⅰ)求该椭圆的离心率和标准方程;(Ⅱ)过
是面积为4的直角三角形。(Ⅰ)求该椭圆的离心率和标准方程;(Ⅱ)过 作直线交椭圆于
作直线交椭圆于 ,
, ,求△
,求△ 的面积
的面积