题目内容
 已知椭圆的中心为原点O,一个焦点为F(
已知椭圆的中心为原点O,一个焦点为F(| 3 |
| ||
| 2 |
| 2 |
(1)求椭圆和圆O的方程;
(2)线段CD恰好被椭圆三等分,求直线l的方程.
分析:(1)根据椭圆的焦点为F(
,0),离心率为
,可得椭圆的几何量,从而可得椭圆的方程,利用以原点为圆心的圆O与直线y=x+4
相切,可得圆的半径,从而可圆的而发愁;
(2)设直线l的方程为y=kx,代入椭圆方程,求得A,B的坐标,求出|AB|,利用线段CD恰好被椭圆三等分,建立方程,可得k的值,从而可求直线l的方程.
| 3 |
| ||
| 2 |
| 2 |
(2)设直线l的方程为y=kx,代入椭圆方程,求得A,B的坐标,求出|AB|,利用线段CD恰好被椭圆三等分,建立方程,可得k的值,从而可求直线l的方程.
解答:解:(1)∵椭圆的焦点为F(
,0),离心率为
,∴c=
,
=
∴a=2,b=
=1
∴椭圆的方程为
+y2=1
∵以原点为圆心的圆O与直线y=x+4
相切
∴圆O的半径为
=4
∴圆O的方程为x2+y2=16;
(2)设直线l的方程为y=kx,代入椭圆方程可得
+(kx)2=1
∴x=±
,∴y=±k
∴A(
,k
),B(-
,-k
),
∴|AB|=
∵线段CD恰好被椭圆三等分,
∴
=
×8
∴
=
,
∴k=±
∴直线l的方程为y=±
x.
| 3 |
| ||
| 2 |
| 3 |
| c |
| a |
| ||
| 2 |
∴a=2,b=
| a2-c2 |
∴椭圆的方程为
| x2 |
| 4 |
∵以原点为圆心的圆O与直线y=x+4
| 2 |
∴圆O的半径为
4
| ||
|
∴圆O的方程为x2+y2=16;
(2)设直线l的方程为y=kx,代入椭圆方程可得
| x2 |
| 4 |
∴x=±
|
|
∴A(
|
|
|
|
∴|AB|=
|
∵线段CD恰好被椭圆三等分,
∴
|
| 1 |
| 3 |
∴
|
| 2 |
| 3 |
∴k=±
| ||
| 7 |
∴直线l的方程为y=±
| ||
| 7 |
点评:本题考查椭圆、圆的方程,考查直线与椭圆的位置关系,考查学生的计算能力,属于中档题.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案
相关题目
 ,长轴在
,长轴在 轴上,上顶点为
轴上,上顶点为 ,左、右焦点分别为
,左、右焦点分别为 ,线段
,线段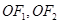 的中点分别为
的中点分别为 ,且△
,且△ 是面积为4的直角三角形。(Ⅰ)求该椭圆的离心率和标准方程;
是面积为4的直角三角形。(Ⅰ)求该椭圆的离心率和标准方程; 作直线
作直线 交椭圆于
交椭圆于 ,
, ,求直线
,求直线
 ,长轴在
,长轴在 轴上,上顶点为
轴上,上顶点为 ,左、右焦点分别为
,左、右焦点分别为 ,线段
,线段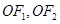 的中点分别为
的中点分别为 ,且△
,且△ 是面积为4的直角三角形。(Ⅰ)求该椭圆的离心率和标准方程;(Ⅱ)过
是面积为4的直角三角形。(Ⅰ)求该椭圆的离心率和标准方程;(Ⅱ)过 作直线交椭圆于
作直线交椭圆于 ,
, ,求△
,求△ 的面积
的面积