题目内容
已知:在平面直角坐标系xOy中,二次函数y=x2-(m+1)x-m-2的图象与x轴交于A、B两点,点A在x轴的负半轴,点B在x轴的正半轴,与y轴交于点C,且OB=3OA.(1)求这个二次函数的解析式;
(2)设抛物线的顶点为D,过点A的直线
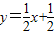 与抛物线交于点E.问:在抛物线的对称轴上是否存在这样的点F,使得△ABE与以B、D、F为顶点的三角形相似,若存在,求出点F的坐标;若不存在,请说明理由;
与抛物线交于点E.问:在抛物线的对称轴上是否存在这样的点F,使得△ABE与以B、D、F为顶点的三角形相似,若存在,求出点F的坐标;若不存在,请说明理由;(3)点G(x,1)在抛物线上,求出过点A、B、G的圆的圆心的坐标.
【答案】分析:解:(1)由题设条件,设A(-x,0),B(3x,0)(x>0),则 ,由A(-x,0),知
,由A(-x,0),知 ,由此能求出这个二次函数的解析式.
,由此能求出这个二次函数的解析式.
(2)由这个二次函数的解析式为y=x2-2x-3,知A(-1,0),B(3,0),D(1,-4),对称轴为直线x=1.由 ,得到点E的坐标为(
,得到点E的坐标为( ).过点E作EH⊥x轴于H.在Rt△AEH中,可求AE=
).过点E作EH⊥x轴于H.在Rt△AEH中,可求AE= ,若对称轴与直线
,若对称轴与直线 交于点P,P点坐标为(1,1).由∠PAM=∠MDB,知要使得在抛物线的对称轴上存在点F,使得△ABE与以B、D、F为顶点的三角形相似,只需要
交于点P,P点坐标为(1,1).由∠PAM=∠MDB,知要使得在抛物线的对称轴上存在点F,使得△ABE与以B、D、F为顶点的三角形相似,只需要 或
或 .由此能求出符合题意的F点坐标.
.由此能求出符合题意的F点坐标.
(3)由点G(x,1)在抛物线上,知点G的坐标为(1 ,1),由A、B、G在同一圆上,知圆心一定在抛物线的对称轴上,由PA=PA=PG=
,1),由A、B、G在同一圆上,知圆心一定在抛物线的对称轴上,由PA=PA=PG= ,知点P即为过点A、B、G的圆的圆心.
,知点P即为过点A、B、G的圆的圆心.
解答:解:(1)由题设条件,设A(-x,0),B(3x,0)(x>0),
则 ,
,
∴由A(-x,0),知 ,
,
即3m2+2m-5=0,
解得m=1,或m=- (舍).
(舍).
∴这个二次函数的解析式为y=x2-2x-3.
(2)在抛物线的对称轴上存在这样的点F,使得△ABE与以B、D、F为顶点的三角形相似.∵这个二次函数的解析式为y=x2-2x-3,
∴A(-1,0),B(3,0),D(1,-4),
对称轴为直线x=1.
∵过点A的直线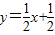 与抛物线交于点E,
与抛物线交于点E,
∴ ,
,
解得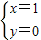 或
或 ,
,
∴点E的坐标为( ).
).
过点E作EH⊥x轴于H
在Rt△AEH中,可求AE= .
.
若对称轴与直线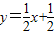 交于点P,
交于点P,
∴P点坐标为(1,1)
∵对称轴与x轴垂直,交点为点M,
∴在Rt△BMD中,可求BD=2 ,
,
在Rt△APM中, ,
,
在Rt△BMD中, ,
,
∴∠PAM=∠MDB.
由题意,要使得在抛物线的对称轴上存在点F,使得△ABE与以B、D、F为顶点的三角形相似,只需要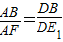 或
或 .
.
∴ ,
,
解得 ,
,
∴点F1 的坐标为(1, ).
).
或 ,
,
解得 D ,
,
∴点F2 的坐标为(1,- ).
).
综上,符合题意的F点坐标为 .
.
(3)∵点G(x,1)在抛物线上
∴点G的坐标为(1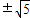 ,1),
,1),
又∵A、B、G在同一圆上
∴圆心一定在抛物线的对称轴上
∵PA=PA=PG=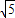 ,
,
∴点P即为过点A、B、G的圆的圆心
∴点P的坐标为(1,1).
点评:本题主要考查二次函数的性质和应用,直线与圆的位置关系,圆的简单性质等基础知识.考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.
 ,由A(-x,0),知
,由A(-x,0),知 ,由此能求出这个二次函数的解析式.
,由此能求出这个二次函数的解析式.(2)由这个二次函数的解析式为y=x2-2x-3,知A(-1,0),B(3,0),D(1,-4),对称轴为直线x=1.由
 ,得到点E的坐标为(
,得到点E的坐标为( ).过点E作EH⊥x轴于H.在Rt△AEH中,可求AE=
).过点E作EH⊥x轴于H.在Rt△AEH中,可求AE= ,若对称轴与直线
,若对称轴与直线 交于点P,P点坐标为(1,1).由∠PAM=∠MDB,知要使得在抛物线的对称轴上存在点F,使得△ABE与以B、D、F为顶点的三角形相似,只需要
交于点P,P点坐标为(1,1).由∠PAM=∠MDB,知要使得在抛物线的对称轴上存在点F,使得△ABE与以B、D、F为顶点的三角形相似,只需要 或
或 .由此能求出符合题意的F点坐标.
.由此能求出符合题意的F点坐标.(3)由点G(x,1)在抛物线上,知点G的坐标为(1
 ,1),由A、B、G在同一圆上,知圆心一定在抛物线的对称轴上,由PA=PA=PG=
,1),由A、B、G在同一圆上,知圆心一定在抛物线的对称轴上,由PA=PA=PG= ,知点P即为过点A、B、G的圆的圆心.
,知点P即为过点A、B、G的圆的圆心.解答:解:(1)由题设条件,设A(-x,0),B(3x,0)(x>0),
则
 ,
,∴由A(-x,0),知
 ,
,即3m2+2m-5=0,
解得m=1,或m=-
 (舍).
(舍).∴这个二次函数的解析式为y=x2-2x-3.
(2)在抛物线的对称轴上存在这样的点F,使得△ABE与以B、D、F为顶点的三角形相似.∵这个二次函数的解析式为y=x2-2x-3,
∴A(-1,0),B(3,0),D(1,-4),
对称轴为直线x=1.
∵过点A的直线
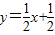 与抛物线交于点E,
与抛物线交于点E,∴
 ,
,解得
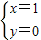 或
或 ,
,∴点E的坐标为(
 ).
).过点E作EH⊥x轴于H
在Rt△AEH中,可求AE=
 .
. 若对称轴与直线
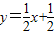 交于点P,
交于点P,∴P点坐标为(1,1)
∵对称轴与x轴垂直,交点为点M,
∴在Rt△BMD中,可求BD=2
 ,
,在Rt△APM中,
 ,
,在Rt△BMD中,
 ,
,∴∠PAM=∠MDB.
由题意,要使得在抛物线的对称轴上存在点F,使得△ABE与以B、D、F为顶点的三角形相似,只需要
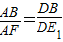 或
或 .
.∴
 ,
,解得
 ,
,∴点F1 的坐标为(1,
 ).
).或
 ,
,解得 D
 ,
,∴点F2 的坐标为(1,-
 ).
).综上,符合题意的F点坐标为
 .
.(3)∵点G(x,1)在抛物线上
∴点G的坐标为(1
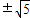 ,1),
,1),又∵A、B、G在同一圆上
∴圆心一定在抛物线的对称轴上
∵PA=PA=PG=
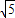 ,
,∴点P即为过点A、B、G的圆的圆心
∴点P的坐标为(1,1).
点评:本题主要考查二次函数的性质和应用,直线与圆的位置关系,圆的简单性质等基础知识.考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.

练习册系列答案
相关题目
 [选做题]在A、B、C、D四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内.
[选做题]在A、B、C、D四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内.