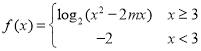题目内容
【题目】已知函数![]() ,
,![]()
(1)判断函数![]() 在区间
在区间![]() 上零点的个数;
上零点的个数;
(2)函数![]() 在区间
在区间![]() 上的极值点从小到大分别为
上的极值点从小到大分别为![]() ,
,![]() ,证明:
,证明:![]() .
.
【答案】(1)两个
(2)证明见解析
【解析】
(1)先由原函数求出其导函数,再研究导函数在![]() ,
,![]() ,
,![]() 的符号问题,从而得出函数
的符号问题,从而得出函数![]() 在区间
在区间![]() 上的单调性,从而得出函数
上的单调性,从而得出函数![]() 在区间
在区间![]() 上零点的个数;
上零点的个数;
(2)先求出函数![]() 的导函数,再结合(1)的结论及正切函数的性质可得
的导函数,再结合(1)的结论及正切函数的性质可得![]() ,再结合余弦函数的单调性即可得解.
,再结合余弦函数的单调性即可得解.
解:(1)因为![]() ,所以
,所以![]() ,
,
当![]() 时,
时,![]() ,
,
![]() 在
在![]() 上单调递减,
上单调递减,![]() ,
,![]() 在
在![]() 上无零点;
上无零点;
当![]() 时,
时,![]() ,
,
![]() 在
在![]() 上单调递增,
上单调递增,![]() ,
,
![]() 在
在![]() 上有唯一零点;
上有唯一零点;
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,
![]() ,
,![]() 在
在![]() 上有唯一零点,
上有唯一零点,
综上,函数![]() 在区间
在区间![]() 上有两个零点;
上有两个零点;
(2)因为![]() ,所以
,所以![]() ,
,
由(1)知![]() 在
在![]() 无极值点;在
无极值点;在![]() 有极小值点,即为
有极小值点,即为![]() ;
;
在![]() 有极大值点,即为
有极大值点,即为![]() ,
,
由![]() ,
,![]() ,
,
![]()
![]() 以及
以及![]() 的单调性,
的单调性,
![]() ,
,
![]() ,由函数
,由函数![]() 在
在![]() 单调递增,
单调递增,
得![]() ,
,
![]() ,
,
由![]() 在
在![]() 单调递减得
单调递减得![]() ,
,
即![]() ,
,
故![]() .
.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
【题目】某公司为强化自己的市场竞争地位,决定扩大公司规模,拓展业务,建立连锁公司,连锁公司利润的20%归总公司,建立连锁公司的数量与单个公司月平均利润的关系如下表所示:
连锁公司数量 | 5 | 6 | 7 | 8 | 9 |
单个公司月平均利润 | 8 | 6 | 4.5 | 3.5 | 3 |
由相关系数![]() 可以反映两个变量相关性的强弱,
可以反映两个变量相关性的强弱,![]() ,认为变量相关性很强;
,认为变量相关性很强;![]() ,认为变量相关性一般;
,认为变量相关性一般;![]() ,认为变量相关性较弱.
,认为变量相关性较弱.
(1)计算相关系数![]() ,并判断变量
,并判断变量![]() 、
、![]() 相关性强弱;
相关性强弱;
(2)求![]() 关于
关于![]() 的线性回归方程
的线性回归方程
(3)若一个地区连锁公司的前期投入![]() (十万元)与数量
(十万元)与数量![]() 的关系为
的关系为![]() ,根据所求回归方程从公司利润角度帮公司对一个地区连锁公司数量做出决策.
,根据所求回归方程从公司利润角度帮公司对一个地区连锁公司数量做出决策.
附注:参考数据:![]() ,
,
参考公式:相关系数 ,
,
线性回归方程![]() 中,
中,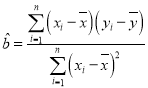 ,
,![]() .
.