题目内容
已知P为抛物线y=2x2+1上的动点，定点A（0，-1），点M分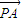
所成的比为2，则点M的轨迹方程为（ ）A．y=6x2-
B．x=6y2-
C．y=3x2+
D．y=-3x2-1
【答案】分析：设出M的坐标，利用点M分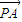
所成的比为2，求出P的坐标，代入抛物线方程即可．
解答：解：设M（x，y）、p（x′，y′），由题意可知
，即：
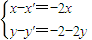，所以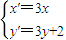
，
因为p（x′，y′）在抛物线上，所以3y+2=2（3x）2+1 所以点M的轨迹方程为：y=6x2-
故选A
点评：本题是基础题，考查圆锥曲线的轨迹方程的求法，注意相关点法的应用．
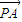所成的比为2，求出P的坐标，代入抛物线方程即可．解答：解：设M（x，y）、p（x′，y′），由题意可知
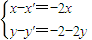，即：，所以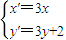，因为p（x′，y′）在抛物线上，所以3y+2=2（3x）2+1 所以点M的轨迹方程为：y=6x2-
故选A
点评：本题是基础题，考查圆锥曲线的轨迹方程的求法，注意相关点法的应用．
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
相关题目
已知P为抛物线y=2x2+1上的动点，定点A（0，-1），点M分
所成的比为2，则点M的轨迹方程为（ ）
| PA |
A、y=6x2-
| ||
B、x=6y2-
| ||
C、y=3x2+
| ||
| D、y=-3x2-1 |