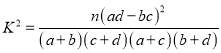题目内容
【题目】已知抛物线![]() :
: ![]() 的焦点为
的焦点为![]() ,圆
,圆![]() :
: ![]() ,过
,过![]() 作垂直于
作垂直于![]() 轴的直线交抛物线
轴的直线交抛物线![]() 于
于![]() 、
、![]() 两点,且
两点,且![]() 的面积为
的面积为![]() .
.
(1)求抛物线![]() 的方程和圆
的方程和圆![]() 的方程;
的方程;
(2)若直线![]() 、
、![]() 均过坐标原点
均过坐标原点![]() ,且互相垂直,
,且互相垂直, ![]() 交抛物线
交抛物线![]() 于
于![]() ,交圆
,交圆![]() 于
于![]() ,
, ![]() 交抛物线
交抛物线![]() 于
于![]() ,交圆
,交圆![]() 于
于![]() ,求
,求![]() 与
与![]() 的面积比的最小值.
的面积比的最小值.
【答案】(1) 抛物线方程为: ![]() ,圆方程为:
,圆方程为: ![]() (2) 当
(2) 当![]() 时,
时, ![]() 与
与![]() 的面积比的取到最小值4.
的面积比的取到最小值4.
【解析】试题分析:(1)先求得![]() 的坐标,可得
的坐标,可得![]() ,由
,由![]() 的面积为
的面积为![]() ,可得
,可得![]() ,从而可得抛物线
,从而可得抛物线![]() 的方程,进而可得圆
的方程,进而可得圆![]() 的方程;(2)设
的方程;(2)设![]() 的方程为
的方程为![]() ,
,
则![]() 方程为
方程为![]() .由
.由![]() 得
得![]() =0,或
=0,或![]()
![]()
![]() 同理可求得
同理可求得![]() .
.
根据弦长公式及点到直线距离公式可得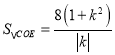 ,
, ![]() ,从而
,从而![]() ,利用基本不等式可得结果.
,利用基本不等式可得结果.
试题解析:(1)因为抛物线焦点F坐标为![]() , 则
, 则![]() ,
,
联立 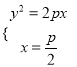 ∴
∴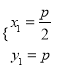 或
或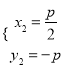 ,
,
故![]() ,
,
∴![]() ,
,
即![]() ,
,
∴抛物线方程为: ![]() .
.
圆方程为: ![]() ,
,
(2) 显然![]() 、
、![]() 的斜率必须存在且均不为0,设
的斜率必须存在且均不为0,设![]() 的方程为
的方程为![]() ,
,
则![]() 方程为
方程为![]() .(注:末说明斜率不给分)
.(注:末说明斜率不给分)
由![]() 得
得![]() =0,或
=0,或![]()
![]()
![]() 同理可求得
同理可求得![]() .
.
则![]()
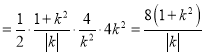 .
.
设![]() 到
到![]() 、
、![]() 的距离分别为
的距离分别为![]() 、
、![]() ,
,
则![]() ;
; ![]() .
.
则![]() .
.
∴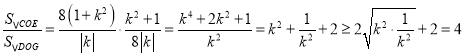 .
.
当且仅当![]() 时,
时, ![]() 与
与![]() 的面积比的取到最小值4.
的面积比的取到最小值4.
【方法点晴】本题主要考查待定系数法求椭抛物线方程及圆锥曲线求最值,属于难题.解决圆锥曲线中的最值问题一般有两种方法:一是几何意义,特别是用圆锥曲线的定义和平面几何的有关结论来解决,非常巧妙;二是将圆锥曲线中最值问题转化为函数问题,然后根据函数的特征选用参数法、配方法、判别式法、三角函数有界法、函数单调性法以及均值不等式法,本题(2)就是用的这种思路,利用均值不等式法求三角形面积比的最值的.

 快捷英语周周练系列答案
快捷英语周周练系列答案【题目】随着共享单车的成功运营,更多的共享产品逐步走入大家的世界,共享汽车、共享篮球、共享充电宝等各种共享产品层出不穷.某公司随即抽取![]() 人对共享产品是否对日常生活有益进行了问卷调查,并对参与调查的
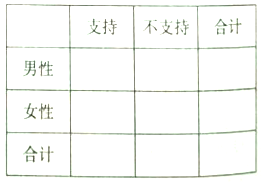
人对共享产品是否对日常生活有益进行了问卷调查,并对参与调查的![]() 人中的性别以及意见进行了分类,得到的数据如下表所示:
人中的性别以及意见进行了分类,得到的数据如下表所示:
男 | 女 | 总计 | |
认为共享产品对生活有益 |
|
|
|
认为共享产品对生活无益 |
|
|
|
总计 |
|
|
|
(1)根据表中的数据,能否在犯错误的概率不超过![]() 的前提下,认为对共享产品的态度与性别有关系?
的前提下,认为对共享产品的态度与性别有关系?
(2)现按照分层抽样从认为共享产品增多对生活无益的人员中随机抽取![]() 人,再从
人,再从![]() 人中随机抽取
人中随机抽取![]() 人赠送超市购物券作为答谢,求恰有
人赠送超市购物券作为答谢,求恰有![]() 人是女性的概率.
人是女性的概率.
参与公式: 
临界值表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|